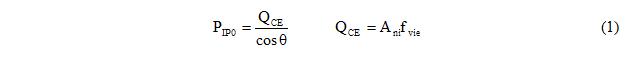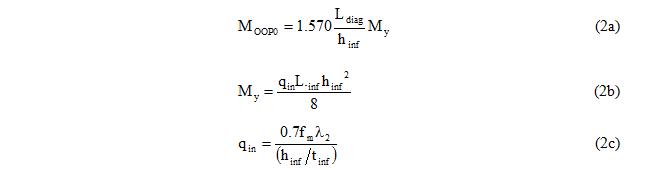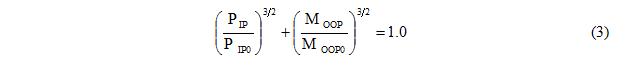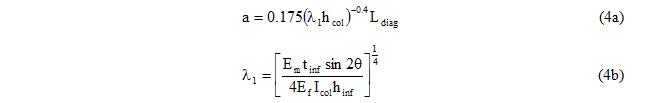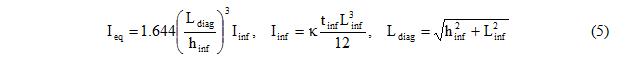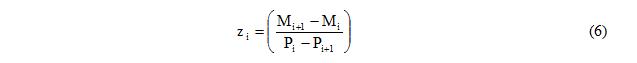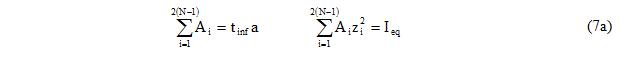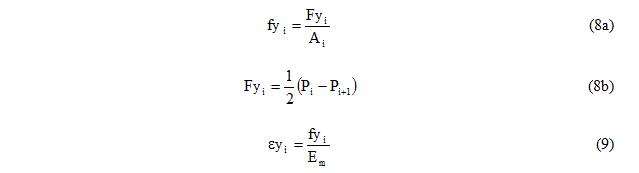Infill Wall Model and Element Removal
M. Selim Gunay and Khalid M. Mosalam, University of California, Berkeley
This article describes the commands for modeling an infill wall element which considers in-plane and out-of-plane interaction and for removal of the element during nonlinear time history simulation in OpenSees. In addition, the infill wall model and element removal algorithm are briefly described. Interested readers can refer to the mentioned references for more information. Questions or comments can be directed to selimgunay [at] berkeley . edu or mosalam [at] ce . berkeley . edu
Note: This article is best viewed with Mozilla Firefox.
Modeling of the Infill Wall
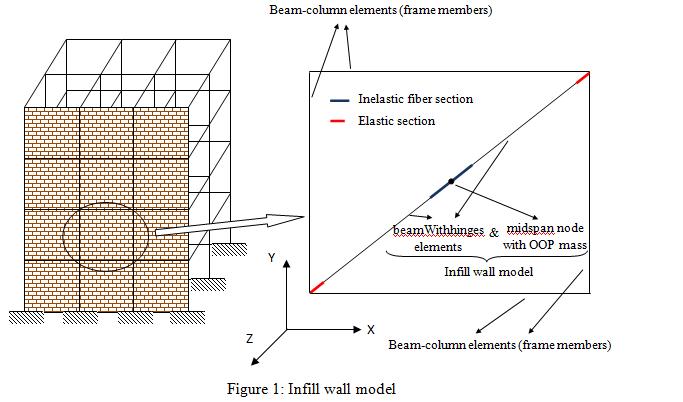
The described infill wall model is a model which considers the interaction of in-plane (IP) and out-of-plane (OOP) effects. Modeling of the infill wall is performed by using the available OpenSees materials, sections, elements and tcl commands. The infill wall model is comprised of two equal size diagonal beamWithhinges elements and a midspan node with OOP mass (Figure 1). The inelastic fiber section assigned to the ends of the elements connected to the midspan node is discretized as explained in the following paragraph. Elastic sections with very small moment of inertia (to simulate moment release) are assigned to the ends attached to the surrounding frame. The hinge length near the midspan node is selected as short as possible in order to produce a relatively sharp yield point for the element, while at the same time providing a numerically stable solution. 1/10 of the total length of the diagonal is a suitable value for the total hinge length (sum of the lengths of the hinges on both sides of the node). The hinge length on the other end can be selected as small as possible without losing numerical stability.
Discretization of Inelastic Fiber Section and Calculation of OOP mass
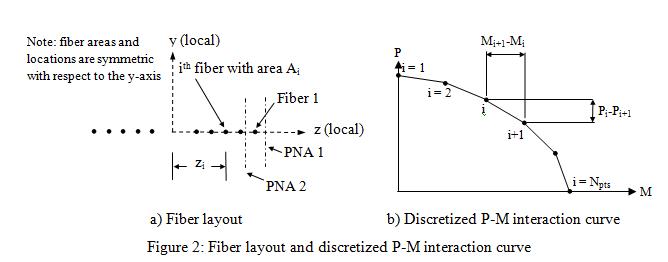
The inelastic fiber section of the beamWithhinges element is modeled by strategically locating a collection of nonlinear fiber elements[1,2]. The fibers are located along a line in the OOP direction (Z-direction in Figure 1). By this way, the beam-column element acts as a truss element and a flexural element in the IP and OOP directions, respectively. The discretization of the cross section is shown in Figure 2a. In this figure, the vector used to define the local-coordinate system in OpenSees, “vecxz”, is (0 0 -1) corresponding to the global axes shown in Figure 1. Each fiber is defined with the area <math>\mathrm{A_i}\,</math>, z-coordinate <math>\mathrm{z_i}\,</math> and a bilinear stress-strain relationship. The strain hardening slope is chosen to be very small, hence the yield stress <math>\mathrm{f_{yi}}\,</math> and the yield strain <math>\mathrm{{\epsilon}_{yi}}\,</math> define the stress-strain relationship of the <math>\mathrm{i_{th}}\,</math> fiber. Since only one diagonal is utilized in the model, it has both tension and compression strengths. Therefore, the fibers are considered to have the same absolute value for the tensile and compression yield strengths.
The parameters defining a fiber section (<math>\mathrm{A_i}\,</math>, <math>\mathrm{z_i}\,</math>, <math>\mathrm{f_{yi}}\,</math>, and <math>\mathrm{{\epsilon}_{yi}}\,</math>) are set such that the intended strength interaction (Figure 2b) and the IP axial and OOP bending stiffness values of the diagonal infill wall element are properly simulated. In the current formulation, FEMA-356[3] or ASCE-41[4] equations are used for calculating the axial stiffness and unidirectional strength in the IP direction. However, any other relationships that the user considers as suitable can also be employed. The OOP mass, stiffness and unidirectional bending strength are calculated such that the model has the same natural frequency as the original infill wall, it should produce the same support reactions where it is attached to the surrounding frame for a given support motion (story acceleration), and it should exhibit initial yielding at the same level of support motion that causes the original infill wall to yield. Discretization of the inelastic fiber section is explained below. In the explanation, equations of FEMA-356 are referred to rather than ASCE-41 equations, since FEMA-356 document is accessible from FEMA website. However, Equations of FEMA-356 and ASCE-41 are very similar and ASCE-41 equations may be replaced with FEMA-356 equations.
1. Calculate the IP axial force capacity of the equivalent diagonal element (<math>\mathrm{P_{IP0}}\,</math>), Equation 1.
In Equation 1, <math>\mathrm{\Theta}\,</math> is the angle of the equivalent diagonal element with the horizontal. <math>\mathrm{Q_{CE}}\,</math> is the expected infill shear strength, <math>\mathrm{A_{ni}}\,</math> is the area of net mortared/grouted section across infill panel and <math>\mathrm{f_{ive}}\,</math> is the expected shear strength of masonry infill. Second part of Equation 1 corresponds to Equation 7-15 in FEMA-356.
2. Calculate the OOP moment capacity under zero IP axial force (MOOP0) for the equivalent diagonal element, Equation 2.
In Equation 2, <math>\mathrm{L_{diag}}\,</math> is the length of the equivalent diagonal element and <math>\mathrm{h_{inf}}\,</math>, <math>\mathrm{L_{inf}}\,</math> and <math>\mathrm{t_{inf}}\,</math> are the height, length and thickness of the infill wall panel, respectively. <math>\mathrm{q_{in}}\,</math> is the OOP strength of the infill wall panel, <math>\mathrm{f_{m}}\,</math> is the expected value of masonry compressive strength and <math>\mathrm{{\lambda}_2}\,</math> is a slenderness parameter defined in Table 7-11 of FEMA-356. Equation 2c corresponds to Equation 7-21 in FEMA-356.
Equation 2 is based on the assumption that the yield moment in the equivalent diagonal element is reached when the support spectral acceleration equals the yield spectral acceleration of the original infill wall. Derivation of Equation 2 can be found in Appendix D of reference [1].
3. Construct the IP axial and OOP bending strength interaction curve accepted as a 3/2-power curve[1, 2] represented with Equation 3. The 3/2 power curve is based on the OOP and IP capacity points obtained from the analyses of a nonlinear finite element (FE) model of an infill panel[3]. In Equation 3, <math>\mathrm{P_{IP}}\,</math> is the IP axial strength in the presence of OOP force, <math>\mathrm{P_{IP0}}\,</math>, which is calculated in step 1, is the IP axial strength without OOP force, <math>\mathrm{M_{OOP}}\,</math> is the OOP bending strength in the presence of IP force, and <math>\mathrm{M_{OOP0}}\,</math>, which is calculated in step 2, is the OOP bending strength without IP force.
It should be noted that steps 1, 2 and 3 consist of the construction of the IP axial and OOP bending strength interaction based on the explained methodology. The user is free to use any other interaction curve which might be based on experimental data or FE simulations, as long as the chosen interaction curve is not concave, since the equations used for calculation of the fiber locations are not suitable for concave diagrams. However, this limitation is not considered to be serious, since a concave interaction diagram is rarely encountered.
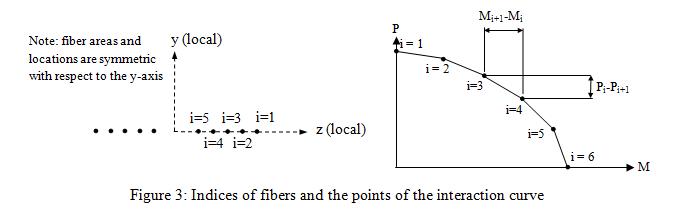
The interaction diagram should be discretized at N pairs (N pairs including the (<math>\mathrm{M_{OOP0}}\,</math>, 0) and (0, <math>\mathrm{P_{IP0}}\,</math>) pairs), where 2(N-1) is the total number of fibers in the section (N-1 fibers are placed at one side of the y-axis and N-1 fibers on the other side symmetrically as shown in Figure 2). Typically, 10 fibers along the section could be sufficient which corresponds to 6 data pairs on the interaction diagram.
4. Calculate the equivalent strut width “a” using Equation 4, which corresponds to Equation 7-14 in FEMA-356. Then, cross-sectional area of the diagonal element becomes tinf×a. The user is free to use any other relationship to calculate the area of the equivalent diagonal element or the equivalent width.
where <math>\mathrm{h_{col}}\,</math> is the height of the column of the surrounding frame, <math>\mathrm{E_{m}}\,</math> and <math>\mathrm{E_{f}}\,</math> are the elasticity moduli of the infill and frame materials, respectively. Equation 4 is unit dependent where force is in kips and displacement is in inches.
5. Calculate the equivalent moment of inertia of the diagonal element in the OOP direction, <math>\mathrm{I_{eq}}\,</math>. Considering that the model has the same natural frequency as the original infill wall and it should produce the same support reactions where it is attached to the frame for a given story acceleration, <math>\mathrm{I_{eq}}\,</math> is calculated with Equation 5.
where <math>\mathrm{\kappa}\,</math> is a factor which represents the reduction in moment of inertia due to cracking.
6. Calculate the distance of the <math>\mathrm{i^{th}}\,</math> fiber to the centroid (<math>\mathrm{z_{i}}\,</math>), Equation 6.
where M and P represent the OOP bending moment and IP axial force capacities in the interaction diagram (Figure 3). i=1 corresponds to the fiber farthest from the centroid and the point of pure compression on the P−M diagram. The index i increases sequentially in the section as progressing inward to the y-axis and in the interaction diagram in the direction of decreasing P as shown in Figure 3. It should be noted that the coordinates of the points (<math>\mathrm{z_{i}}\,</math>) on one side of the y axis (positive z) are calculated with Equation 6 but coordinates of the points on the other side are calculated as the negative of the values calculated with Equation 6.
Equation 6 is obtained from the consideration of the changes in the plastic axial force and moment that occur as the plastic neutral axis is “swept through” the section. Derivation of this equation is explained in reference [2].
7. Area of each fiber is calculated such that the sum of the areas of the fibers is equal to the cross sectional area of the equivalent diagonal element (<math>\mathrm{t_{inf}}\,</math>×a) calculated in step 4 and sum of the second moment of the fibers is equal to the equivalent moment of inertia in OOP direction (<math>\mathrm{I_{eq}}\,</math>) calculated in step 5.
In order to have a unique solution of Equation 7a, the relationship between <math>\mathrm{A_{i}}\,</math> and <math>\mathrm{z_{i}}\,</math> is assumed to be represented with Equation 7b.
since <math>\mathrm{z_{i}}\,</math> values are known from Equation 6, <math>\mathrm{\gamma}\,</math> and <math>\mathrm{\eta}\,</math> can be determined from Equation 7. Then, the area of each fiber is calculated using Equation 7b.
8. Calculate yield stress and yield strain for each fiber, Equations 8 and 9.
Equation 8b is obtained from the consideration of the change in the plastic axial force that occurs as the plastic neutral axis (PNA in Figure 2) is “swept through” the section. Derivation of this equation is explained in reference [2].
9. In addition to the fibers along z direction, a dummy fiber (a fiber with a very small area) should be located at an arbitrary point along the y-axis (Figure 2) to supply a very small IP moment of inertia.
The inelastic fiber section is discretized following the above nine steps. Cross sectional area obtained in step 4 and moment of inertia in OOP direction obtained in step 5 are used as area and moment of inertia about the local axis corresponding to the OOP direction for the interior elastic part of the beamWithhinges element. A very small number is input for the moment of inertia about the other sectional local axis.
Calculation of OOP Mass at the Midspan Node
As stated previously, the described infill wall element is comprised of two equal size diagonal beamWithhinges elements and a midspan node with OOP mass. This mass at the midspan node is calculated as 0.81M, where M is the total mass of the infill wall panel. This value is the first mode effective mass of the infill wall panel when it is defined as a beam spanning vertically with distributed mass and with simple supports at the ends. Theoretical derivation can be found in reference [1].
Implementation of Infill Wall Removal in OpenSees
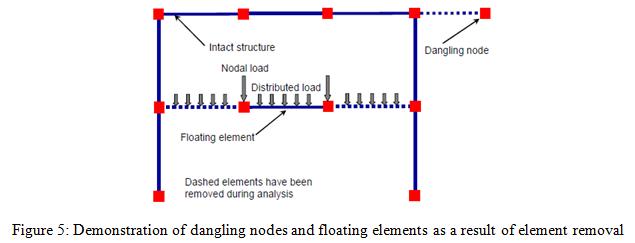
A progressive collapse algorithm is developed [4-6], the different applications of which can be found in references [7-10]. This algorithm is developed using element removal based on dynamic equilibrium and resulting transient change in system kinematics, the underlying theory of which can be found in the above references. The progressive collapse algorithm is implemented for automated removal of collapsed elements during an ongoing simulation (Figure 4). The implementation is carried out as a new OpenSees module, designed so that it is called by the main analysis module after each converged load step to check each element for possible violation of its respective removal criteria. A violation of any pre-defined removal criterion triggers the activation of the element removal algorithm on the violating element before returning to the main analysis module. Activation of the element removal algorithm includes updating nodal masses, checking if the removal of the collapsed element results in leaving behind dangling nodes or floating elements, which must be removed as well (Figure 5), and removing all associated element and nodal forces, imposed displacements, and constraints.
Other than the aforementioned infill wall element, removal criteria are defined for force- and displacement-based distributed plasticity fiber elements and lumped plasticity beam–column elements with fiber-discretized plastic hinges. These criteria are based on material-level damage indices for a newly developed confined RC cross-section model [11-13]. The removal of the latter elements are not considered in the current version of OpenSees. However, they will be available in near future. Current version considers only the removal of the infill wall model described in the first section.
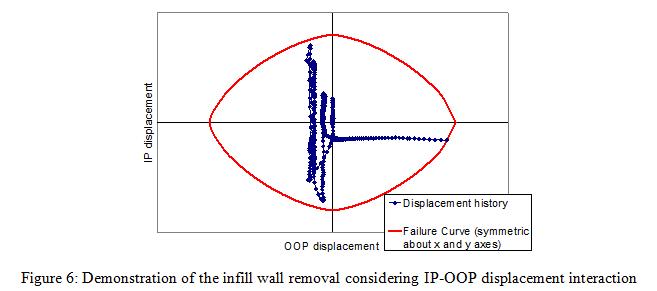
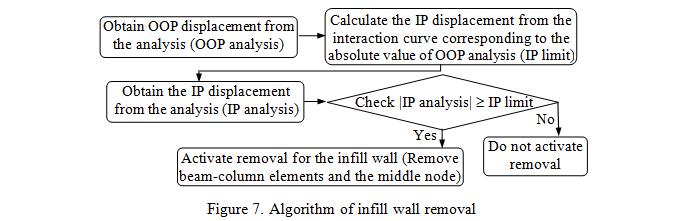
Implementation of the removal of the elements representing the aforementioned infill wall analytical model in the progressive collapse algorithm is performed through defining a removal criterion for the beam-column elements of this model. This criterion is based on the interaction between the IP and OOP displacements. IP displacement is the relative horizontal displacement between the top and bottom nodes of the diagonal element. OOP displacement is that of the middle node (where the OOP mass is attached) with respect to the chord which connects the top and bottom nodes. The user is free to choose any interaction relationship between IP and OOP displacements. In the recent studies conducted with the introduced infill wall element [14, 15], same equation used for the strength interaction is considered for the displacement interaction, where IP and OOP displacement capacities in the presence of zero load in the other direction are obtained from FEMA-356 for collapse prevention level. During the nonlinear time history simulation, when the mentioned combination of displacements from the analysis exceeds the interaction curve (Figure 6), the two beam-column elements and the middle node, representing the unreinforced masonry infill wall, are removed. The procedure for the removal of an infill wall is presented in Figure 7.
New Command in OpenSees Interpreter
The only new tcl command in the OpenSees interpreter with respect to the infill wall removal is the collapse recorder. Three collapse recorders (the syntax of which are indicated below) are needed for the consideration of the removal of an infill wall. These collapse recorders should be defined individually for each infill wall that the user would like to be considered for removal.
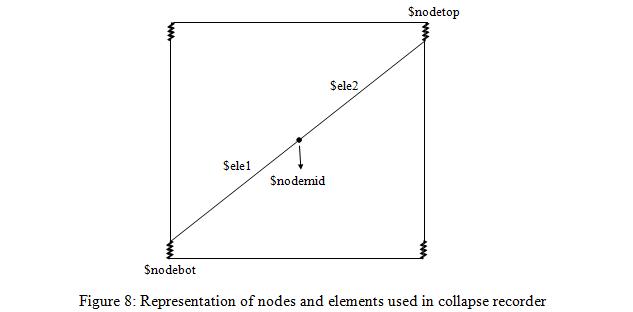
recorder Collapse -ele $ele1 -time -crit INFILLWALL -$file $filename -file_infill $filenameinf -global_gravaxis $globgrav -checknodes $nodebot $nodemid $nodetop recorder Collapse -ele $ele2 -time -crit INFILLWALL -file_infill $filenameinf -global_gravaxis $globgrav -checknodes $nodebot $nodemid $nodetop recorder Collapse -ele $ele1 $ele2 -node $nodemid
$ele1, $ele2, $nodebot, $nodemid, and $nodetop are shown in Figure 8. Element objects store the identities of their associated Node objects in the data structures of OpenSees. Therefore, it might seem that node inputs are unnecessary. However, when there are shear springs in the model, $nodetop and $nodebot should be the nodes of the springs which connect to the beams, since the shear spring deformation contributes to the IP displacement of the infill wall. These nodes are not the nodes of the diagonal element. Therefore, it is necessary to input these nodes. $filename is the file name for element removal log. Only one log file is constructed for all collapse recorder commands (i.e. for all removals). The first file name input to a collapse recorder command is used and any subsequent file names are ignored. $filenameinf is the file used to input the displacement interaction curve. Two columns of data are input in this file where only positive values are input. First column is the OOP displacement in ascending order and second column is the corresponding IP displacement. Full interaction should be defined. In other words, first value of OOP displacement and last value of IP displacement should be zero. –crit INFILLWALL is used to state that the removal is for the infill wall, because there will be options for removal of other elements in the next versions of OpenSees as mentioned previously. $globgrav is the global axis of the model in the direction of gravity. 1, 2 and 3 should be input for X, Y and Z axes, respectively. For example, it is equal to 2 in Figure 1.
Example
Files related to the example can be downloaded from the links below. This example is based on "Example 8. generic 3D Frame, NStory NBayX NBayZ, Reinforced-Concrete Section" which is available in OpenSees Examples Manual. Main file is "Model_IR.tcl". Lines 326-469 in this file are related to the infill wall model and element removal. File which conducts time history analysis is NRHA_IR.tcl. Ground motion files (PUL194.tcl, PUL104.tcl) should be located under a directory named "GMFiles". Calculation of the infill wall parameters are summarized in the file Calculations.pdf. This file is created using Mathcad originally by Stephen Kadysiewski. Interested users can request the Mathcad file by sending email to selimgunay [at] berkeley . edu or mosalam [at] ce . berkeley . edu
Files
- Model_IR.tcl
- NRHA_IR.tcl
- ReadSMDFile_IR.tcl
- LibAnalysisDynamicParameters_IR.tcl
- DisplayModel3D_IR.tcl
- DisplayPlane_IR.tcl
- BuildRCrectSection_IR.tcl
- LibMaterialsRC_IR.tcl
- LibUnits_IR.tcl
- Dispwall1-cg.tcl
- PUL194.tcl
- PUL104.tcl
- Calculations.pdf
References
1. Kadysiewski, S. and Mosalam, K.M. (2009), “Modeling of Unreinforced Masonry Infill Walls Considering In-plane and Out-of-Plane Interaction”, Pacific Earthquake Engineering Research Center, PEER 2008/102.
2. Kadysiewski, S. and Mosalam, K.M. (2009), “Modelling of Unreinforced Masonry Infill Walls Considering In-Plane and Out-of-Plane Interaction”, Proceedings of the 11th Canadian Masonry Symposium, Toronto, Ontario, May 31-June 6.
3. Hashemi, S.A. and Mosalam, K.M. (2007), “Seismic Evaluation of Reinforced Concrete Buildings Including Effects of Infill Masonry Walls”, Pacific Earthquake Engineering Research Center, PEER 2007/100.
4. Talaat, M. and Mosalam, K.M. (2008), “Computational Modeling of Progressive Collapse in Reinforced Concrete Frame Structures”, Pacific Earthquake Engineering Research Center, PEER 2007/10.
5. Talaat, M. and Mosalam, K.M. (2009), “Modeling Progressive Collapse in Reinforced Concrete Buildings Using Direct Element Removal”, Earthquake Engineering and Structural Dynamics, 38(5): 609-634.
6. Talaat, M. and K. M. Mosalam, K.M. (2009), Chapter20: How to Simulate Column Collapse and Removal in As-built and Retrofitted Building Structures?, in Seismic Risk Assessment and Retrofitting - with special emphasis on existing low-rise structures, Ilki, A, Karadogan, F, Pala, S & Yuksel, E (Eds), ISBN 978-90-481-2680-4, Springer.
7. Talaat, M. and Mosalam, K.M. (2006), “Progressive Collapse Modeling of Reinforced Concrete Framed Structures Containing Masonry Infill Walls”, Proceedings of the 2nd NEES/E-Defense Workshop on Collapse Simulation of Reinforced Concrete Building Structures, Kobe, Japan.
8. Talaat, M. and Mosalam, K.M. (2007), “Towards Modeling Progressive Collapse in Reinforced Concrete Buildings”, Proceedings of SEI-ASCE 2007 Structures Congress, Long Beach, California, USA.
9. Mosalam, K.M., Talaat, M., and Park, S. (2008), “Modeling Progressive Collapse in Reinforced Concrete Framed Structures”, Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, October 12-17, Paper S15-018.
10. Mosalam, K.M., Park, S., Günay, M.S. (2009), “Evaluation of an Element Removal Algorithm for Reinforced Concrete Structures Using Shake Table Experiments,” Proceedings of the 2nd International Conference on Computational Methods in structural Dynamics and Earthquake Engineering (COMPDYN 2009), Island of Rhodes, Greece, June 22-24.
11. Binici, B. and Mosalam, K.M. (2007), “Analysis of Reinforced Concrete Columns Retrofitted With Fiber Reinforced Polymer Lamina,” Composites Part B: Engineering, 38(2): 265-276.
12. Mosalam, K.M., Talaat, M., and Binici, B. (2007), “A Computational Model for Reinforced Concrete Members Confined with Fiber Reinforced Polymer Lamina: Implementation and Experimental Validation,” Composites Part B: Engineering, 38(5-6): 598-613.
13. Mosalam, K.M., Talaat, M., and Binici, B. (2007), “Computational Model for FRP-Confined RC Members”, Proceedings of the 8th International Symposium on Fiber Reinforced Polymer Reinforcement for Concrete Structures (FRPRCS-8), University of Patras, Patras, Greece.
14. Mosalam, K.M., and Günay, S. (2010), Chapter 33: Seismic Retrofit of Non-Ductile Reinforced Concrete Frames Using Infill Walls as a Rocking Spine, in Advances in Performance-Based Earthquake Engineering, Geotechnical, Geological, and Earthquake Engineering, Fardis, M.N. (Ed.), Springer.
15. Günay, S., Korolyk, M., Mar D., Mosalam, K.M., and Rodgers, J. (2009), “Infill Walls as a Spine to Enhance the Seismic Performance of Non-Ductile Reinforced Concrete Frames,” Proceedings of the ATC&SEI Conference on Improving the Seismic Performance of Existing Buildings and Other Structures, December 9-11, San Francisco, California.