Concrete04 Material -- Popovics Concrete Material

This command is used to construct a uniaxial Popovics concrete material object with degraded linear unloading/reloading stiffness according to the work of Karsan-Jirsa and tensile strength with exponential decay.

uniaxialMaterial Concrete04 $matTag $fc $ec $ecu $Ec <$fct $et> <$beta>

---

$matTag	integer tag identifying material
$fc	floating point values defining concrete compressive strength at 28 days (compression is negative)*
$ec	floating point values defining concrete strain at maximum strength*
$ecu	floating point values defining concrete strain at crushing strength*
$Ec	floating point values defining initial stiffness**
$fct	floating point value defining the maximum tensile strength of concrete
$et	floating point value defining ultimate tensile strain of concrete
$beta	loating point value defining the exponential curve parameter to define the residual stress (as a factor of $ft) at $etu

NOTE:

• Compressive concrete parameters should be input as negative values.
• The envelope of the compressive stress-strain response is defined using the model proposed by Popovics (1973). If the user defines Ec = 57000*sqrt(|fcc|)(in psi)' then the envelope curve is identical to proposed by Mander et al. (1988).
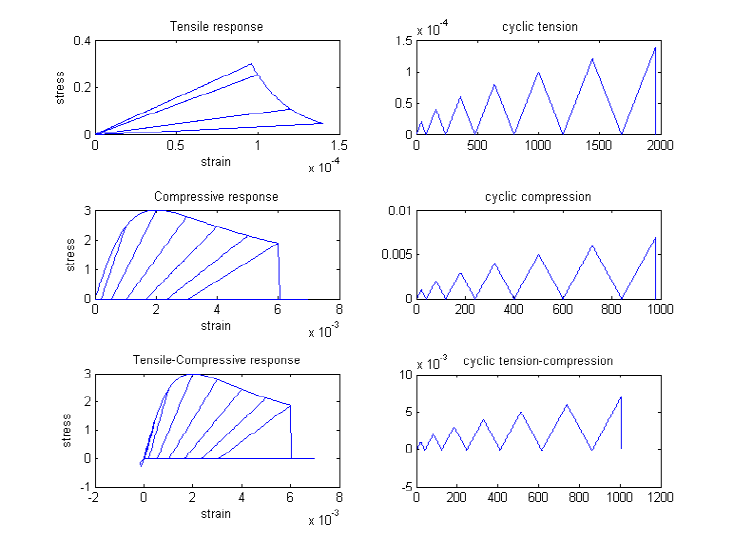
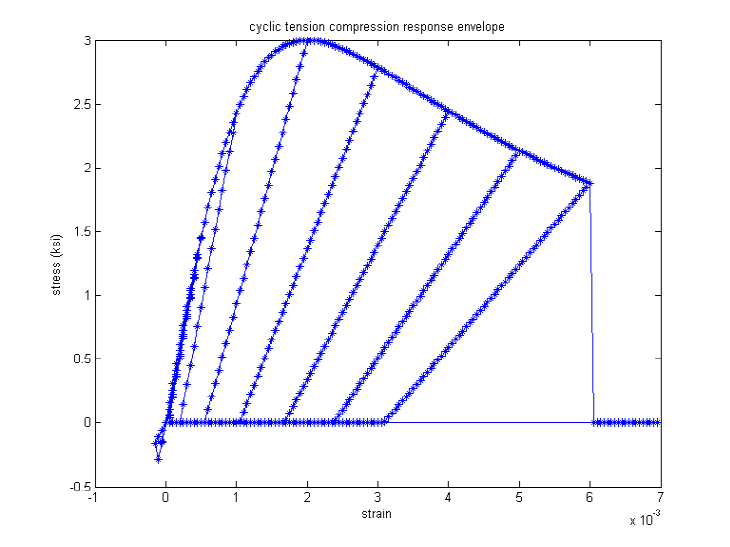
• Model Characteristic: For loading in compression, the envelope to the stress-strain curve follows the model proposed by Popovics (1973) until the concrete crushing strength is achieved and also for strains beyond that corresponding to the crushing strength. For unloading and reloading in compression, the Karsan-Jirsa model (1969) is used to determine the slope of the curve. For tensile loading, an exponential curve is used to define the envelope to the stress-strain curve. For unloading and reloading in tensile, the secant stiffness is used to define the path.

REFERENCES: Reference:

• Mander, J. B., Priestley, M. J. N., and Park, R. (1988). "Theoretical stress-strain model for confined concrete." Journal of Structural Engineering ASCE, 114(8), 1804-1825.

• Popovics, S. (1973). " A numerical approach to the complete stress strain curve for concrete." Cement and concrete research, 3(5), 583-599.

• Karsan, I. D., and Jirsa, J. O. (1969). "Behavior of concrete under compressive loading." Journal of Structural Division ASCE, 95(ST12).

---

Code Developed by: Laura Lowes, University of Washington and Michael Berry, University of Washington

Images Developed by: Silvia Mazzoni