Example 1: 2D soil column subjected to earthquake base excitation
Created by: Quan Gu (Xiamen University, China), Joel P. Conte (UCSD), Michele Barbato (LSU), Yong Li (UCSD)
Return to Sensitivity Analysis Demonstration Examples Page
This example is taken as a 3-D three-story reinforced concrete frame structure with rigid diaphragm behavior at each floor, subjected to bidirectional earthquake base excitation with ground acceleration time histories taken as the two horizontal components of the 1978 Tabas earthquake.
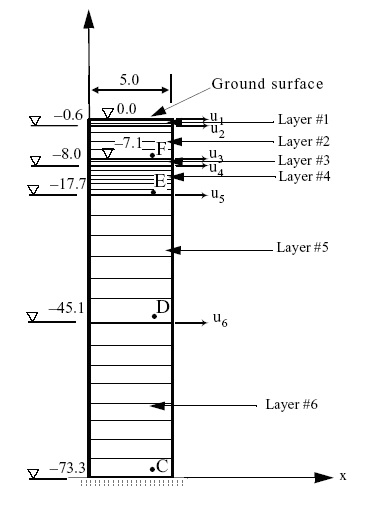
Figure 1 Layered soil column subjected to total base acceleration with finite element mesh in thin lines (unit: m)
Figure 2 Total acceleration time history at the base of the soil column
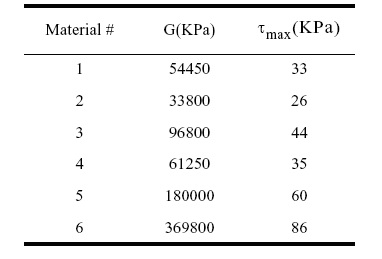
Figure 3 Material properties of various layers of soil column (from ground surface to base of soil column)
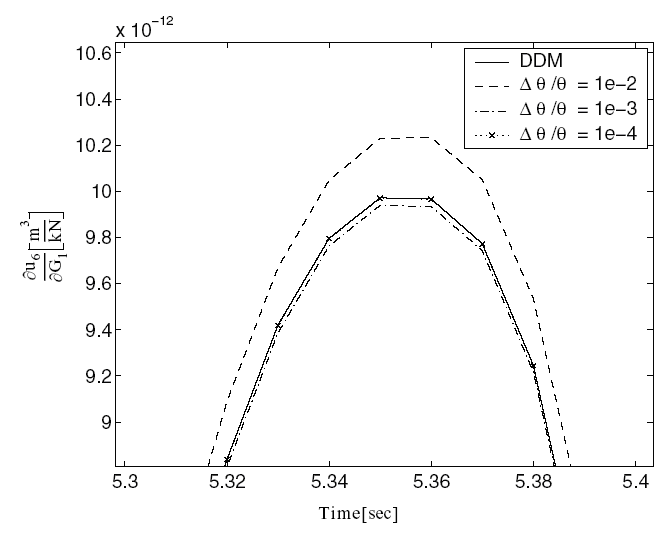
To run this example, the user needs to run Example1_soil2D.tcl in OpenSees to perform FE response and response sensitivity analysis. To verify the DDM results of the nodal horizontal displacement at node 29 (u6 in Figure 2.1) with respect to parameter G1 of the top soil layer (layer #1) using forward finite difference (FFD)analysis, the user needs to run Example1_soil2D_FFD.tcl. Finally, the user needs to run in Matlab Example1_cmp.m to visualize the results.
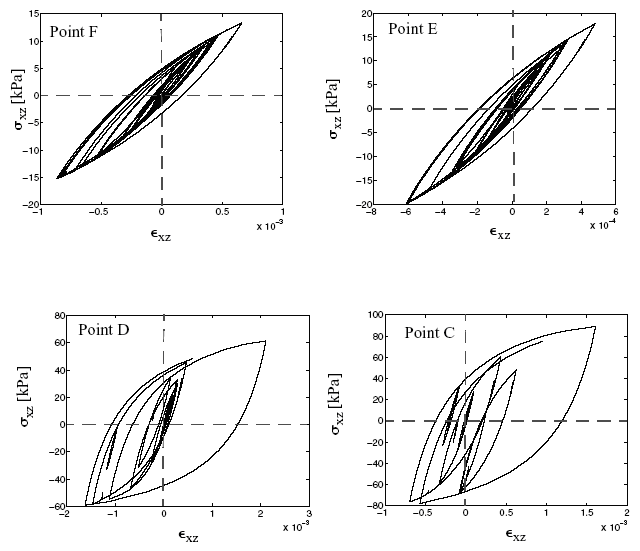
Figure 4 Shear stress–strain hysteric responses at Gauss points C, D, E, and F (see Figure 1)
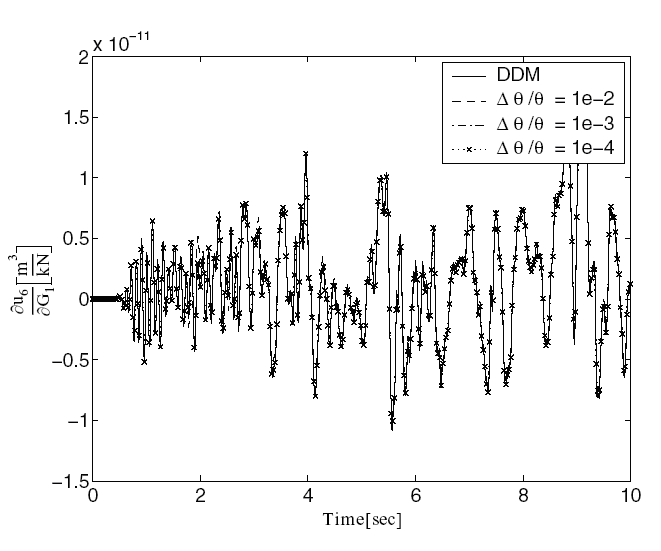
Figure 5 Sensitivity of displacement response u6 (see Figure 2.1) to shear modulus G1 obtained using DDM and forward finite difference with increasingly small perturbations of sensitivity parameter
Figure 6 Sensitivity of displacement response u6 to shear modulus G1 obtained using DDM and forward finite difference with increasingly small perturbations of sensitivity parameter (zoom view)
Tcl Input File Download
To execute this analysis in OpenSees the user has to download this input file:
Reference
Gu Q., Conte J.P., Elgamal A., Yang Z. (2009) “Response sensitivity analysis of a multi-yield-surface J2 plasticity model by direct differentiation method.” Computer Methods in Applied Mechanics and Engineering, 198(30-32):2272-2285.