PressureDependMultiYield02-Example 3

Command_Manual
- Tcl Commands
- Modeling_Commands
  - model
  - uniaxialMaterial
  - ndMaterial
  - frictionModel
  - section
  - geometricTransf
  - element
  - node
  - sp commands
    - fix
    - fixX
    - fixY
    - fixZ
  - mp commands
  - timeSeries
  - pattern
  - mass
  - block commands
    - block2D
    - block3D
  - region
  - rayleigh
- Analysis Commands
- Output Commands
  - recorder
  - record
  - print
  - printA
  - logFile
  - RealTime_Output_Commands
- Misc Commands
- DataBase Commands
  - Template:DataBaseCommandsMenu

Solid-fluid fully coupled (u-p) 20-8 noded brick element: saturated soil element with pressure dependent material, subjected to 1D sinusoidal base shaking

Input File

# single 20_8_BrickUP element with pressure dependent material.
# subjected to 1D sinusoidal base shaking 

# Written by Jinchi Lu (May 2004)

set matOpt   1      ;# 1 = pressure depend; 
                    ;# 2 = pressure independ; 
wipe

set friction 31.         ;#friction angle
set phaseTransform 26.   ;#phase transformation angle
set G1 9.e4 ;
set B1 22.e4 ;
set gamma    0.600      ;# Newmark integration parameter



set dT   0.01           ;# time step for analysis, does not have to be the same as accDt.
set numSteps 2500       ;# number of time steps
set rhoS  1.80          ;# saturated mass density
set rhoF  1.00          ;# fluid mass density

set Bfluid 2.2e6        ;# fluid shear modulus
set fluid1 1            ;# fluid material tag
set solid1 10           ;# solid material tag
set perm   1.e-5    ;#permeability (m/s)
set accGravity 9.81  ;#acceleration of gravity
set perm   [expr $perm/$accGravity/$rhoF]    ;# actual value used in computation

set accMul 2                    ;# acceleration multiplier 
set pi 3.1415926535                     ;
set inclination 0;

set massProportionalDamping   0.0 ;
set InitStiffnessProportionalDamping 0.003;

set gravityX [expr $accGravity*sin($inclination/180.0*$pi)] ;# gravity acceleration in X direction
set gravityY 0.0                                        ;# gravity acceleration in Y direction
set gravityZ [expr -$accGravity*cos($inclination/180.0*$pi)]  ;# gravity acceleration in Z direction

set ndm    3            ;# space dimension


model BasicBuilder -ndm 3 -ndf 4
node        1      0.00000     0.0000    0.00000
node        2      1.00000     0.0000    0.00000
node        3      1.00000     1.0000    0.00000
node        4      0.00000     1.0000    0.00000
node        5      0.00000     0.0000    1.00000
node        6      1.00000     0.0000    1.00000
node        7      1.00000     1.0000    1.00000
node        8      0.00000     1.0000    1.00000

fix      1      1      1      1   0
fix      2      1      1      1   0 
fix      3      1      1      1   0
fix      4      1      1      1   0
fix      5      0      1      0   1
fix      6      0      1      0   1
fix      7      0      1      0   1
fix      8      0      1      0   1


model BasicBuilder -ndm 3 -ndf 3

node        9      0.50000     0.0000    0.00000
node       10      1.00000     0.5000    0.00000
node       11      0.50000     1.0000    0.00000
node       12      0.00000     0.5000    0.00000
node       13      0.50000     0.0000    1.00000
node       14      1.00000     0.5000    1.00000
node       15      0.50000     1.0000    1.00000
node       16      0.00000     0.5000    1.00000
node       17      0.00000     0.0000    0.50000
node       18      1.00000     0.0000    0.50000
node       19      1.00000     1.0000    0.50000
node       20      0.00000     1.0000    0.50000

fix      9      1      1      1    
fix     10      1      1      1    
fix     11      1      1      1    
fix     12      1      1      1    
fix     13      0      1      0    
fix     14      0      1      0    
fix     15      0      1      0    
fix     16      0      1      0    
fix     17      0      1      0    
fix     18      0      1      0    
fix     19      0      1      0    
fix     20      0      1      0    

# equalDOF
# tied nodes around

equalDOF      5     6  1     3
equalDOF      5     7  1     3
equalDOF      5     8  1     3
equalDOF      5    13  1     3
equalDOF      5    14  1     3
equalDOF      5    15  1     3
equalDOF      5    16  1     3
equalDOF     17    18  1     3
equalDOF     17    19  1     3
equalDOF     17    20  1     3

# define material and properties
switch $matOpt {
  1 {
    nDMaterial PressureDependMultiYield02 1 3 $rhoS $G1 $B1 $friction .1 80 0.5\
                                          $phaseTransform 0.067 0.23 0.06 0.27
  }
  2 {
    nDMaterial PressureIndependMultiYield 2 3 1.8 4.e4 2.e5 40 .1
  }
}

element 20_8_BrickUP   1     1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20  $matOpt $Bfluid $rhoF $perm $perm $perm $gravityX $gravityY $gravityZ 


#recorder for nodal variables along the vertical center line.
set SnodeList {}
for {set i 0} {$i < 20} {incr i 1} {
  lappend SnodeList [expr $i+1]
}

set FnodeList {}
for {set i 0} {$i < 8} {incr i 1} {
  lappend FnodeList [expr $i+1]
}

# GRAVITY APPLICATION (elastic behavior)


numberer Plain
system ProfileSPD
test NormDispIncr 1.0e-8 20 1
algorithm KrylovNewton
constraints Penalty 1.e18 1.e18; #
set nw 1.5
set nw2 [expr pow($nw+0.5, 2)/4]
integrator Newmark $nw $nw2
analysis Transient 

analyze 10 5.e3

# switch the material to plastic
updateMaterialStage -material $matOpt -stage 1
analyze 10 1.e1


setTime 0.0 ;# reset time, otherwise reference time is not zero for time history analysis 
wipeAnalysis

eval "recorder Node -file  disp -time -node $SnodeList -dof 1 2 3  -dT $dT disp"
eval  "recorder Node -file pwp -time -node $FnodeList -dof 4  -dT $dT vel"
eval "recorder Node -file acc  -time -node $SnodeList -dof 1 2 3  -dT $dT accel"
recorder Element -ele 1  -time -file stress1  -dT $dT material 1 stress
recorder Element -ele 1  -time -file strain1  -dT $dT material 1 strain
recorder Element -ele 1  -time -file stress5  -dT $dT material 5 stress
recorder Element -ele 1  -time -file strain5  -dT $dT material 5 strain
recorder Element -ele 1  -time -file stress17  -dT $dT material 17 stress
recorder Element -ele 1  -time -file strain17  -dT $dT material 17 strain

############# create dynamic time history analysis ##################
pattern UniformExcitation 1 1 -accel "Sine 0 10 1 -factor $accMul"

rayleigh $massProportionalDamping 0.0 $InitStiffnessProportionalDamping 0.0
integrator Newmark $gamma  [expr pow($gamma+0.5, 2)/4]  
constraints Penalty 1.e18 1.e18 ;# can't combine with test NormUnbalance   
test NormDispIncr 1.0e-3 25 0   ;# can't combine with constraints Lagrange
#algorithm Newton               ;# tengent is updated at each iteration
algorithm KrylovNewton         ;#  step not each iteration
system ProfileSPD                ;# Use sparse solver. Next numberer is better to be Plain.
numberer Plain                  ;# method to map between between equation numbers of DOFs
analysis VariableTransient      ;# splitting time step requires VariableTransient

############# perform the Analysis and record time used ############# 
set startT [clock seconds]
analyze $numSteps $dT [expr $dT/64] $dT  15
set endT [clock seconds]
puts "Execution time: [expr $endT-$startT] seconds."

MATLAB Plotting File

clear all;

a1=load('acc');
d1=load('disp');
p1=load('pwp');
s1=load('stress1');
e1=load('strain1');
s5=load('stress5');
e5=load('strain5');
s9=load('stress17');
e9=load('strain17');

fs=[0.5, 0.2, 4, 6];
fs2=[0.5, 0.2, 4, 3];
accMul = 2;

%integration point 1 p-q
po=(s1(:,2)+s1(:,3)+s1(:,4))/3;
for i=1:size(s1,1)
    qo(i)=(s1(i,2)-s1(i,3))^2 + (s1(i,3)-s1(i,4))^2 +(s1(i,2)-s1(i,4))^2 + 6.0* (s1(i,5)^2 +s1(i,6)^2+s1(i,7)^2) ;
   qo(i)=sign(s1(i,7))*1/3.0*qo(i)^0.5;
end

figure(1); close 1; figure(1);
%integration point 1 stress-strain
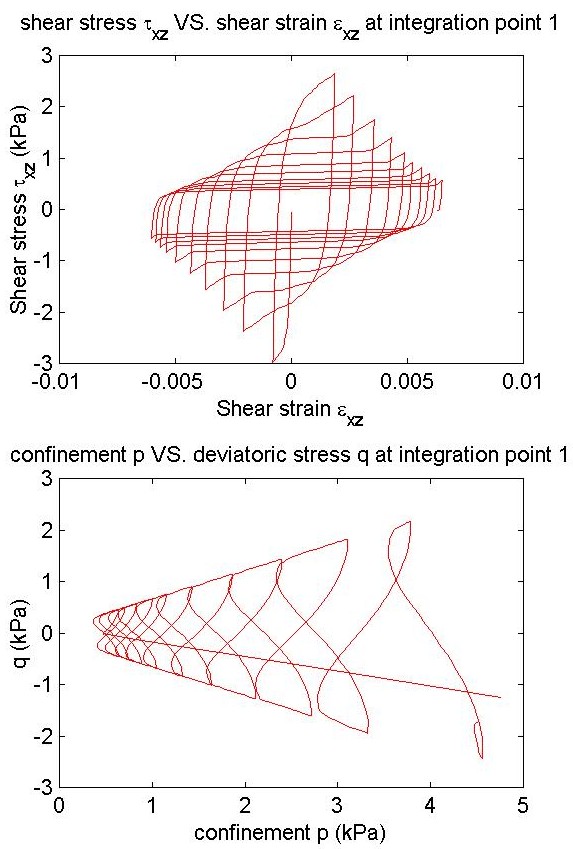
subplot(2,1,1), plot(e1(:,7),s1(:,7),'r');
title ('shear stress \tau_x_z VS. shear strain \epsilon_x_z at integration point 1');
xLabel('Shear strain \epsilon_x_z');
yLabel('Shear stress \tau_x_z (kPa)');
subplot(2,1,2), plot(-po,qo,'r');
title ('confinement p VS. deviatoric stress q at integration point 1');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ_p1','jpg');


%integration point 5 p-q
po=(s5(:,2)+s5(:,3)+s5(:,4))/3;
for i=1:size(s5,1)
    qo(i)=(s5(i,2)-s5(i,3))^2 + (s5(i,3)-s5(i,4))^2 +(s5(i,2)-s5(i,4))^2 + 6.0*( s5(i,5)^2 +  s5(i,6)^2 + s5(i,7)^2);
   qo(i)=sign(s5(i,7))*1/3.0*qo(i)^0.5;
end

figure(5); close 5; figure(5);
%integration point 5 stress-strain
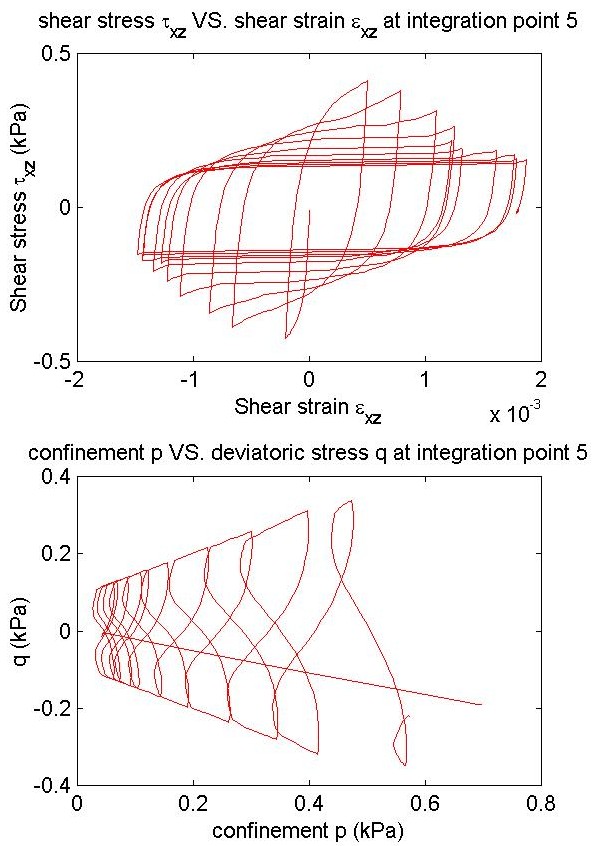
subplot(2,1,1), plot(e5(:,7),s5(:,7),'r');
title ('shear stress \tau_x_z VS. shear strain \epsilon_x_z at integration point 5');
xLabel('Shear strain \epsilon_x_z');
yLabel('Shear stress \tau_x_z (kPa)');
subplot(2,1,2), plot(-po,qo,'r');
title ('confinement p VS. deviatoric stress q at integration point 5');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ_p5','jpg');

%integration point 9 p-q
po=(s9(:,2)+s9(:,3)+s9(:,4))/3;
for i=1:size(s1,1)
    qo(i)=(s9(i,2)-s9(i,3))^2 + (s9(i,3)-s9(i,4))^2 +(s9(i,2)-s9(i,4))^2 + 6.0*( s9(i,5)^2 +  s9(i,6)^2 +  s9(i,7)^2);
   qo(i)=sign(s9(i,7))*1/3.0*qo(i)^0.5;
end

figure(6); close 6; figure(6);
%integration point 9 stress-strain
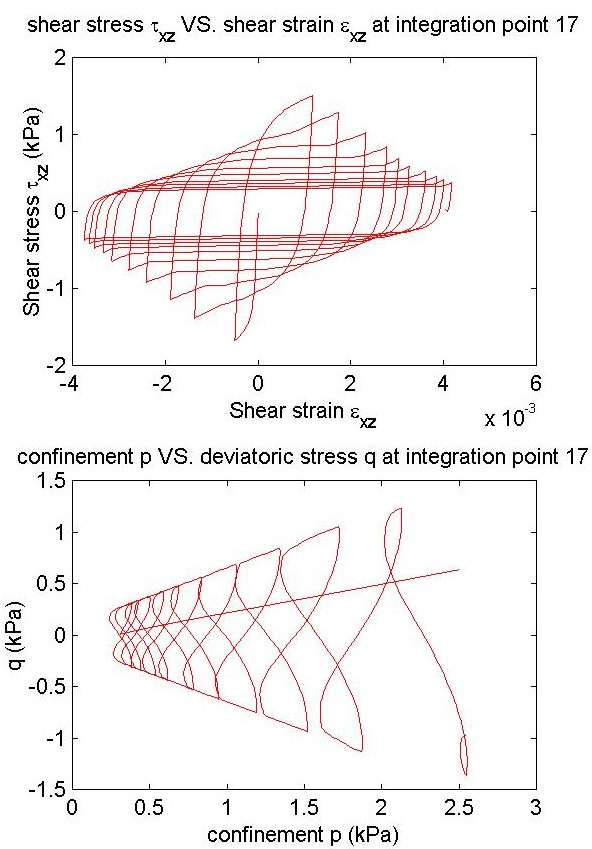
subplot(2,1,1), plot(e9(:,7),s9(:,7),'r');
title ('shear stress \tau_x_z VS. shear strain \epsilon_x_z at integration point 17');
xLabel('Shear strain \epsilon_x_z');
yLabel('Shear stress \tau_x_z (kPa)');
subplot(2,1,2), plot(-po,qo,'r');
title ('confinement p VS. deviatoric stress q at integration point 17');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ_p17','jpg');

figure(2); close 2; figure(2);
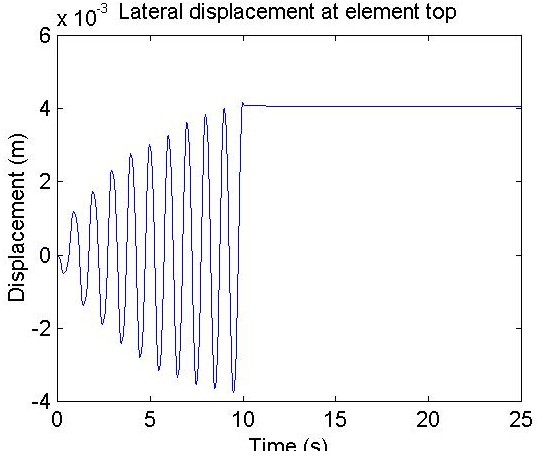
%node 3 displacement relative to node 1
plot(d1(:,1),d1(:,14));
title ('Lateral displacement at element top');
xLabel('Time (s)');
yLabel('Displacement (m)');
set(gcf,'paperposition',fs2);
saveas(gcf,'Disp','jpg');

s=accMul*sin(0:pi/50:20*pi);
s=[s';zeros(3000,1)];
s1=interp1(0:0.01:40,s,a1(:,1));

figure(3); close 3; figure(3);
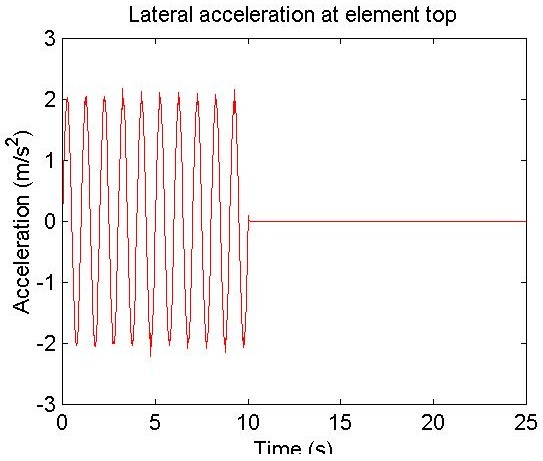
%node acceleration
a = plot(a1(:,1),s1+a1(:,14),'r');
title ('Lateral acceleration at element top');
xLabel('Time (s)');
yLabel('Acceleration (m/s^2)');
set(gcf,'paperposition',fs2);
saveas(gcf,'Acc','jpg');

figure(4); close 4; figure(4);
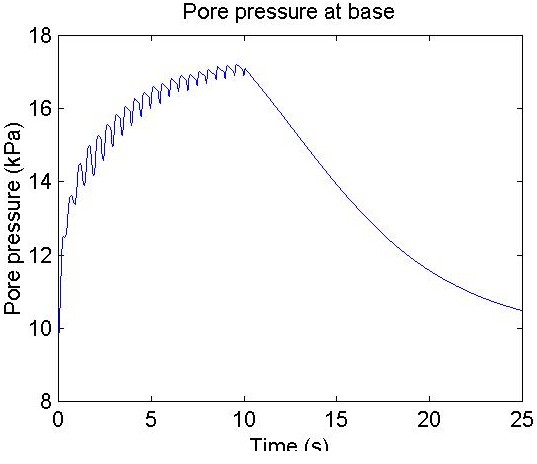
a=plot(p1(:,1),p1(:,2));
title ('Pore pressure at base');
xLabel('Time (s)');
yLabel('Pore pressure (kPa)');
set(gcf,'paperposition',fs2);
saveas(gcf,'EPWP','jpg');