PressureDependMultiYield-Example 1

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

Elastic Pressure Dependent Dry Level Dynamic

Input File

clear all;

a1=load('acce.out');
d1=load('disp.out');
s1=load('stress1.out');
e1=load('strain1.out');
s5=load('stress3.out');
e5=load('strain3.out');

fs=[0.5, 0.2, 4, 6];
accMul = 9.81;

%integration point 1 p-q
po=(s1(:,2)+s1(:,3)+s1(:,4))/3;
for i=1:size(s1,1)
    qo(i)=(s1(i,2)-s1(i,3))^2 + (s1(i,3)-s1(i,4))^2 +(s1(i,2)-s1(i,4))^2 + 6.0* s1(i,5)^2;
    qo(i)=sign(s1(i,5))*1/3.0*qo(i)^0.5;
end
figure(1); clf;
%integration point 1 stress-strain
subplot(2,1,1), plot(e1(:,4),s1(:,5),'r');
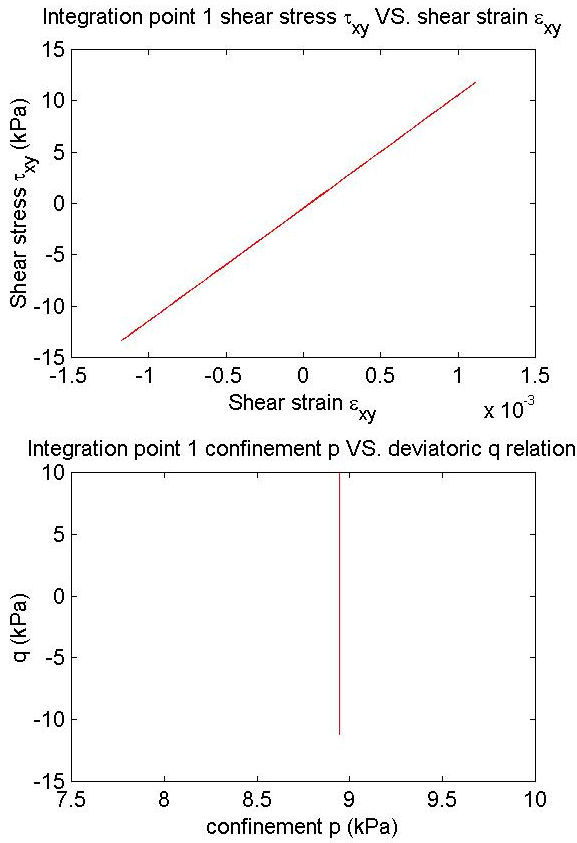
title ('Integration point 1 shear stress \tau_x_y VS. shear strain \epsilon_x_y');
xLabel('Shear strain \epsilon_x_y');
yLabel('Shear stress \tau_x_y (kPa)');

subplot(2,1,2), plot(-po,qo,'r');
title ('Integration point 1 confinement p VS. deviatoric q relation');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ1','jpg');

%integration point 3 p-q
po=(s5(:,2)+s5(:,3)+s5(:,4))/3;
for i=1:size(s5,1)
    qo(i)=(s5(i,2)-s5(i,3))^2 + (s5(i,3)-s5(i,4))^2 +(s5(i,2)-s5(i,4))^2 + 6.0* s5(i,5)^2;
    qo(i)=sign(s5(i,5))*1/3.0*qo(i)^0.5;
end

figure(4); clf;
%integration point 3 stress-strain
subplot(2,1,1), plot(e5(:,4),s5(:,5),'r');
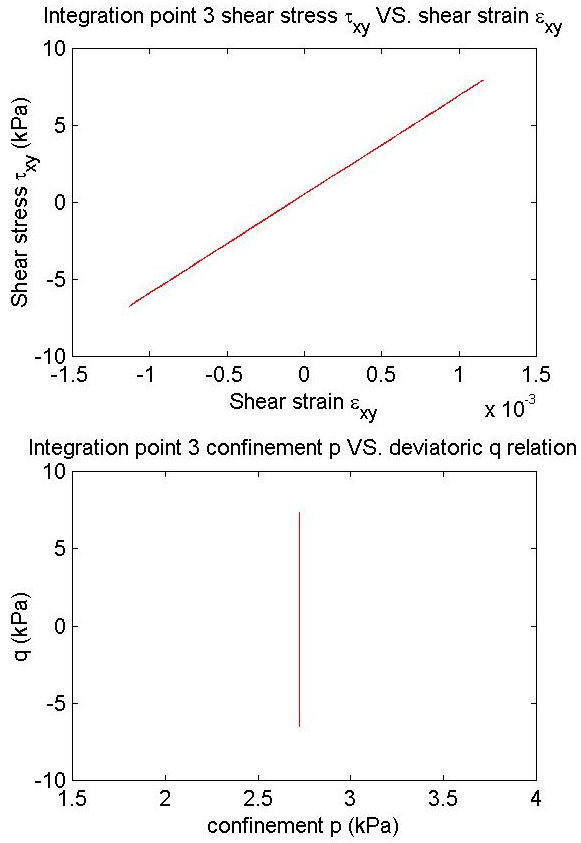
title ('Integration point 3 shear stress \tau_x_y VS. shear strain \epsilon_x_y');
xLabel('Shear strain \epsilon_x_y');
yLabel('Shear stress \tau_x_y (kPa)');

subplot(2,1,2), plot(-po,qo,'r');
title ('Integration point 3 confinement p VS. deviatoric q relation');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ5','jpg');

figure(2); clf;
%node 3 displacement relative to node 1
subplot(2,1,1),plot(d1(:,1),d1(:,6),'r');
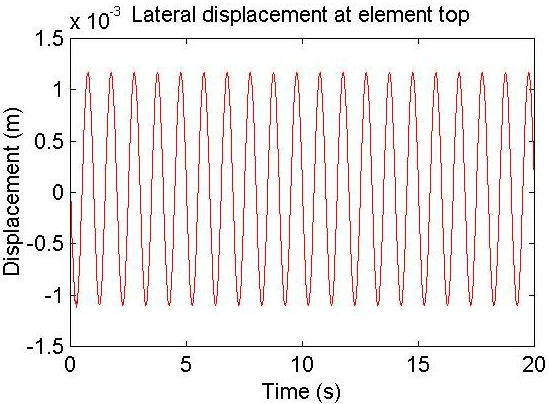
title ('Lateral displacement at element top');
xLabel('Time (s)');
yLabel('Displacement (m)'); 
set(gcf,'paperposition',fs);
saveas(gcf,'D','jpg');


s=accMul*sin(0:pi/50:40*pi);
s1=interp1(0:0.01:20,s,a1(:,1));

figure(1); clf;
%node 3 relative acceleration
subplot(2,1,1),plot(a1(:,1),s1+a1(:,5),'r');
title ('Lateral acceleration at element top');
xLabel('Time (s)');
yLabel('Acceleration (m/s^2)');
set(gcf,'paperposition',fs);
saveas(gcf,'A','jpg');

MATLAB Plotting File

clear all;

a1=load('acce.out');
d1=load('disp.out');
s1=load('stress1.out');
e1=load('strain1.out');
s5=load('stress3.out');
e5=load('strain3.out');

fs=[0.5, 0.2, 4, 6];
accMul = 9.81;

%integration point 1 p-q
po=(s1(:,2)+s1(:,3)+s1(:,4))/3;
for i=1:size(s1,1)
    qo(i)=(s1(i,2)-s1(i,3))^2 + (s1(i,3)-s1(i,4))^2 +(s1(i,2)-s1(i,4))^2 + 6.0* s1(i,5)^2;
    qo(i)=sign(s1(i,5))*1/3.0*qo(i)^0.5;
end
figure(1); clf;
%integration point 1 stress-strain
subplot(2,1,1), plot(e1(:,4),s1(:,5),'r');
title ('Integration point 1 shear stress \tau_x_y VS. shear strain \epsilon_x_y');
xLabel('Shear strain \epsilon_x_y');
yLabel('Shear stress \tau_x_y (kPa)');

subplot(2,1,2), plot(-po,qo,'r');
title ('Integration point 1 confinement p VS. deviatoric q relation');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ1','jpg');

%integration point 3 p-q
po=(s5(:,2)+s5(:,3)+s5(:,4))/3;
for i=1:size(s5,1)
    qo(i)=(s5(i,2)-s5(i,3))^2 + (s5(i,3)-s5(i,4))^2 +(s5(i,2)-s5(i,4))^2 + 6.0* s5(i,5)^2;
    qo(i)=sign(s5(i,5))*1/3.0*qo(i)^0.5;
end

figure(4); clf;
%integration point 3 stress-strain
subplot(2,1,1), plot(e5(:,4),s5(:,5),'r');
title ('Integration point 3 shear stress \tau_x_y VS. shear strain \epsilon_x_y');
xLabel('Shear strain \epsilon_x_y');
yLabel('Shear stress \tau_x_y (kPa)');

subplot(2,1,2), plot(-po,qo,'r');
title ('Integration point 3 confinement p VS. deviatoric q relation');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ5','jpg');

figure(2); clf;
%node 3 displacement relative to node 1
subplot(2,1,1),plot(d1(:,1),d1(:,6),'r');
title ('Lateral displacement at element top');
xLabel('Time (s)');
yLabel('Displacement (m)'); 
set(gcf,'paperposition',fs);
saveas(gcf,'D','jpg');


s=accMul*sin(0:pi/50:40*pi);
s1=interp1(0:0.01:20,s,a1(:,1));

figure(1); clf;
%node 3 relative acceleration
subplot(2,1,1),plot(a1(:,1),s1+a1(:,5),'r');
title ('Lateral acceleration at element top');
xLabel('Time (s)');
yLabel('Acceleration (m/s^2)');
set(gcf,'paperposition',fs);
saveas(gcf,'A','jpg');

Displacement Output File

Stress-Strain Output File (Integration Point 1)

Stress-Strain Output File (Integration Point 3)

Acceleration Output File

---

Return to:

• NDMaterial Command
  • UC San Diego soil models (Linear/Nonlinear, dry/drained/undrained soil response under general 2D/3D static/cyclic loading conditions (please visit UCSD for examples)
    • PressureIndependMultiYield Material
    • PressureDependMultiYield Material
    • PressureDependMultiYield02 Material
    • PressureDependMultiYield03 Material
  • UC San Diego Saturated Undrained soil
    • FluidSolidPorousMaterial

• Element Command
  • UC San Diego u-p element (saturated soil)
    • Four Node Quad u-p Element
    • Brick u-p Element
    • bbarQuad u-p Element
    • bbarBrick u-p Element
    • Nine Four Node Quad u-p Element
    • Twenty Eight Node Brick u-p Element
• Related References

---