Simply supported beam modeled with two dimensional solid elements

Example Provided by: Vesna Terzic, UC Berkeley

---

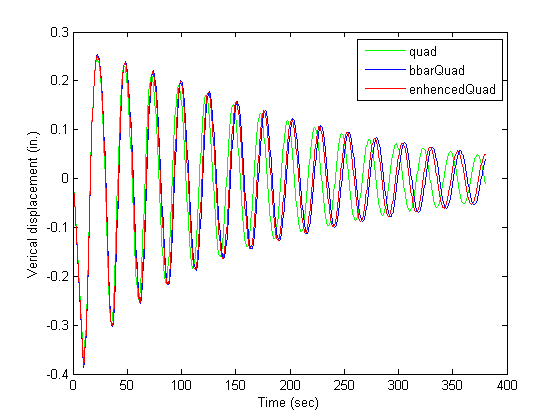
This example (adopted from the old OpenSees Examples Manual) considers a simple problem in solid dynamics. The structure is a simply supported beam modelled with two dimensional solid elements (quadrilateral elements). The beam is first exposed to static load (two nodal loads) and then to free vibrations caused by removal of the static load. Free vibrations of the beam are graphically displayed at the time the beam is analyzed. Three types of quadrilateral elements: quad element, bbarQuad element, and enhencedQuad element are considered in analysis and their results are compared.

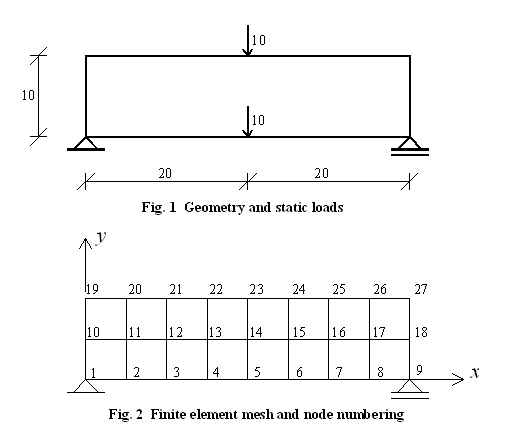
Fig. 1 shows the geometry of the beam and the static load. Units adopted for this example are: kip, inch, sec. Fig. 2 shows the global coordinate system, finite element mesh, and nodal numeration in case the mesh is generated with 8 x 2 elements.

Instructions on how to run this example

To execute this ananlysis in OpenSees download this file: DynAnal_BeamWithQuadElements.tcl

To run this example, place the OpenSees.exe to the same directory with the downloaded file. By double cliking on OpenSees.exe the OpenSees interpreter will pop out. To run the analysis the user sholud type "source Example6_3.tcl" in OpenSees interpreter and hit enter.

Create the model

Spatial dimension of the model and number of degrees-of-freedom (DOF) at nodes are defined using model command. For two-dimensional analysis, a typical solid element is defined as a volume in two-dimensional space. In this example we have 2D model with 2 DOFs at each node. This is defined in the following way:

model BasicBuilder -ndm 2 -ndf 2

The geometry of the beam will be defined and the mesh of quadrilateral elements will be generated using bloc2D command. This command also specifies the type of quadrilateral elements to be used in analysis. In order to define a quadrilateral element we need to create the NDmaterial first. For this example ElasticIsotropic material is used with a modulus of elasticity of 1000 ksi, Poisson's ratio of 0.25, and mass density of 6.75 kip/cu in.

nDMaterial ElasticIsotropic 1 1000 0.25 3.0

Choose the type of quadrilateral element to use in the analysis:

set Quad quad
or
set Quad bbarQuad
or
set Quad enhancedQuad

Arguments for the three types of quadrilateral elements under consideration are defined next. All three elements model plane strain material behavior.

if {$Quad == "enhancedQuad" } {
	set eleArgs "PlaneStrain2D 1"
}
if {$Quad == "quad" } {
	set eleArgs "1 PlaneStrain2D 1"
}
if {$Quad == "bbarQuad" } {
	set eleArgs "1"
}

Number of elements in x and y direction of the beam are set to:

set nx 16
set ny  4

The user can change these values and make the mesh finer or coarser. Number of elements in x direction has to remain even since the forces are applied at the beam centerline.

The nodes and elements are defined next using block2D command.

block2D $nx $ny 1 1 $Quad $eleArgs {
	1  0   0
	2  40  0
	3  40  10
	4  0   10
}

To be able to change the mesh by only changing nx and ny values, numbering of node at the right support (bn) and nodes at the loads application (l1 and l2) are defined as follows:

set bn [expr $nx + 1]
set l1 [expr $nx/2 + 1]
set l2 [expr $l1 + $ny*($nx+1)]

The boundary conditions are defined next using single-point constraint command fix. Node 1 is fixed in both direction and node bn is a roller.

fix   1 1 1
fix $bn 0 1

Define recorders

Vertical displacement at the beam centerline is recorded using node recorder command. The file Node.out (placed in folder Data) will have two columns: the 1st column will be time and the 2nd column will be vertical beam displacement from both, static and transient analysis.

recorder Node -file Data/Node.out -time -node $l1 -dof 2 disp

Create and perform static analysis

To apply static load, a single load pattern with a linear time series and two vertical nodal loads are used.

pattern Plain 1 Linear {
load $l1 0.0 -1.0
load $l2 0.0 -1.0
}

Analysis objects are defined and load is applied in 10 steps of analysis. A solution algorithm of type Newton is used for the problem. The solution algorithm tests the convergence on the norm of the energy increment vector.

integrator LoadControl 1.0 1 1.0 10.0
test EnergyIncr 1.0e-12  10  0
algorithm Newton
numberer RCM
constraints Plain
system ProfileSPD
analysis Static
analyze 10

Create display for transient analysis

The display will be created using recorder display command. Here we specify window title (e.g., "Simply supported Beam"), then x and y location of the top-left corner of the window (relative to the upper-left corner of the screen), and finally width and height of the graphical window in pixels. Projector reference point (prp) is defined next. This point defines the center of projection (viewer's eye) (for more information: Viewpoint Projections and Specifications). Usually it is placed at the center of the object that is to be graphically presented. For this example, the center of the structure is at (20,5) (Figure 1). Next, we have to define view-up (vup) vector. It is are (0,1,0). Window view is defined next using command viewWindow and the four coordinates (-x, x, -y, y) that define the size of the viewing window relative to the prp. In this example the viewing window with its vector (-30, 30, -10, 10) is set to have 10 units of blank space on left and right side of the beam and 5 units of blank space below and above the beam. Finally, we use display command to display the displacements of the beam during transient analysis. The first argument following the command specifies the type of response to be plotted. The second argument following display command is magnification factor for nodes and the third argument is magnification factor for the response quantity to be displayed.

recorder display "Simply Supported Beam" 10 10 800 200 -wipe
prp 20 5.0 1.0
vup 0 1 0
viewWindow -30 30 -10 10
display 10 0 5

Free vibrations of the beam - Transient analysis

Subsequent to the static analysis, the wipeAnalysis command is used to clear analysis objects defined for static analysis. The time is reset to zero and remove loadPatern command is used to remove the nodal loads and create a new analysis. The nodal displacements have not changed. However, with the external loads removed the structure is no longer in static equilibrium.

wipeAnalysis
setTime 0.0
remove loadPattern 1

Damping of the beam elements is defined next. It is stiffness-proportional Rayleigh damping based on the 1st mode. The damping ratio in the first mode is set to 2%.

rayleigh 0. 0. 0. [expr 2*0.02/sqrt([eigen 1])];

The transient analysis objects are defined next. The integrator for the dynamic analysis is Newmark that considers constant average acceleration in one time step of analysis, <math>\gamma = 0.5</math> and <math>\beta = 0.25</math>. This choice is unconditionally stable and energy conserving for linear problems. Additionally, this integrator conserves linear and angular momentum for both linear and non-linear problems. The dynamic analysis is performed using 1500 time increments with a time step of <math>\delta t=0.5</math>.

test EnergyIncr 1.0e-12 10 0
algorithm Newton
numberer RCM
constraints Plain
integrator Newmark 0.5 0.25
system BandGeneral
analysis Transient

analyze 1500 0.5

Results

The figure below shows the vertical displacement at the beam centerline for the three different types of quadrilateral elements. First 10 sec on the figure show the response of the beam to the static load, while the rest of the response corresponds to vibrations caused by the load removal.