Beam With Hinges Element

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

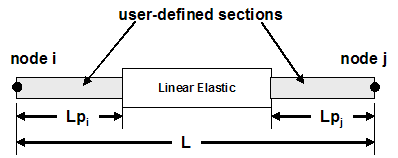
This command is used to construct a beamWithHinges element object, which is based on the non-iterative (or iterative) flexibility formulation, and considers plasticity to be concentrated over specified hinge lengths at the element ends.

For 2D:

element beamWithHinges $eleTag $iNode $jNode $secTagI $Lpi $secTagJ $Lpj $E $A $Iz $transfTag <-mass $massDens> <-iter $maxIters $tol>

For 3D:

element beamWithHinges $eleTag $iNode $jNode $secTagI $Lpi $secTagJ $Lpj $E $A $Iz $Iy $G $J $transfTag <-mass $massDens> <-iter $maxIters $tol>

---

$eleTag	unique element object tag
$iNode $jNode	end nodes
$secTagI	identifier for previously-defined section object at node $iNode
$LpI	plastic hinge length at end i
$secTagJ ...	identifier for previously-defined section object at node $iNode
$LpJ	plastic hinge length at node j
$E	Youngs modulus elastic portion
$A	Area for elastic portion
$Iy	second moment of area for elastic portion about local y
$Iz	second moment of area for elastic portion about local z
$G	torsional moment of inertia of cross section for elastic portion
$J	Shear Modulus of elastic portion.
$transfTag	identifier for previously-defined coordinate-transformation
$maxIters	maximum number of iterations to undertake to satisfy element compatibility (optional, default=1)
$tol	tolerance for satisfaction of element compatibility (optional, default=10-16)
$intType	numerical integration type, options are Lobatto, Legendre, Radau, NewtonCotes, Trapezoidal (optional, default= Lobatto)

NOTE:

1. The beamWithHinges element localize plastic hinging at the element ends only.
2. The valid queries to a nonlinear beam-column element when creating an ElementRecorder object are:
3. The valid responses that an element of this type will respond to are:
   1. forces or globalForces
   2. localForces
   3. basicForces
   4. section $sectionTag $arg1 $arg2 ...
   5. basicDeformations
   6. plasticDeformations
   7. inflectionPoint
   8. tangentDrift
   9. integrationPoints
   10. integrationWeights
4. The section at endI corresponds to section number 1, and the section at end j corresponds to section number 6.

---

DISCUSSION:

Behind the scenes, the element is actually a ForceBeamColumn with nonlinear user defined sections and elastic sections and some clever numerical integration. The implementation divides the element in three parts: two hinges at the ends, and a linear-elastic region in the middle. The hinges are defined by assigning to each a previously-defined section. The length of the each hinge is also specified by the user:

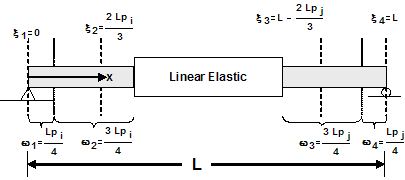
While the integration of distributed-plasticity force-base elements distributes the gauss points along the entire element length, the beamWithHinges element localizes the integration points in the hinge regions. Two integration points per hinge are used to be able represent the curvature distribution accurately -- Gauss-Radau Integration:

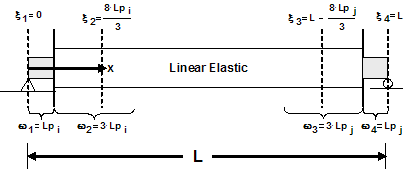
Two integration points per hinge, however, require too much computational overhead. A Modified Gauss-Radau Integration, developed by Scott et al., would apply the Gauss-Radau hinge integration over 4Lp instead of Lp. Elastic properties are then applied to the interior integration points, where a closed-form solution is used:

There are many advantages to this formulation over the standard forceBeamColumnelement:

   # Nonlinear behavior is confined to the integration points at the element ends.
   # The user only needs to specify the length of each hinge.
   # Captures largest bending moment at the ends.
   # Represents linear curvature distributions exactly.
   # Characteristic length is equal to Lp when deformations localize.

EXAMPLE:

REFERENCES:

Scott, M.H. and G.L. Fenves. "Plastic Hinge Integration Methods for Force-Based Beam-Column Elements", Journal of Structural Engineering, ASCE, 132(2):244-252, February 2006.

---

Code Developed by: Micheal Scott, Oregon State University