Time History Analysis of a 2D Elastic Cantilever Column
This page is under construction...
Example Provided by: Vesna Terzic, UC Berkeley
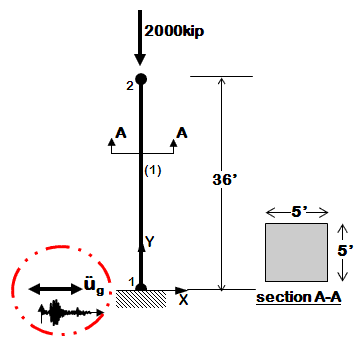
This example demonstrates how to perform time history analysis of a 2D elastic reinforced concrete cantilever column with a gravity load included in the analysis. The column will be exposed only to horizontal component of ground motion. This example is a tutorial for the example Ex1a.Canti2D.EQ.tcl (given in the examples manual) and is intended to help OpenSees beginners get started. Geometry of the cantilever column, node and element numbering are shown in the figure below.
Instructions on how to run this example
To execute this ananlysis in OpenSees the user has to download these files:
- Ex1a.Canti2D.EQ.tcl
- BM68elc.acc (ground-motion file)
Place Ex1a.Canti2D.EQ.tcl and unzipped BM68elc.acc file in the same folder with the OpenSees.exe. By double clicking on OpenSees.exe the OpenSees interpreter will pop out. To run the analysis the user should type:
source Ex1a.Canti2D.EQ.tcl
and hit enter. To create output files (stored in directory "data") the user has to exit OpenSees interpreter by typing "exit".
Create the model
Before creating the model it is advised to call wipe command to destroy all previously constructed objects, i.e. all previously defined components of the model, all previously defined components of the analysis and all previously defined recorders.
The model of a structural system is created in the following way:
1. Spatial dimension of the model (NDM) and number of degrees-of-freedom (DOF) at nodes are defined using model command.
2. Coordinates of the nodes are defined using node command. At this point the user has to choose basic units (e.g., kip, in., sec) and remain consistent while creating the model.
3. If dynamic (transient) analysis is performed nodal mass is assigned using either node or mass command. A mass has to be assigned to each degree of freedom.
4. The boundary conditions are defined using using single-point constraint command fix. For nodes that have some fixity, constraints have to be defined at all degrees of freedom (0 if unconstrained (or free), 1 if constrained (or fixed)). Completely free nodes do not have to be defined.
5. Before element is defined, the geometric transformation of the element has to be defined using geometric transformation command. This command transforms beam element stiffness and resisting force from the basic system to the global-coordinate system. Three types of geometric transformation are available in OpenSees: Linear Transformation, PDelta Transformation, and Corotational Transformation. In a 2D problem, element orientation does not need to be considered, and can be the same for all elements.
6. The elements are to be defined using one of the elements available in OpenSees. For the purpose of this example Elastic Beam Column Element will be used. Different types of elements require different additional commands for their definition.
For the given example, steps from 1 to 6 are explained below. The link to command description is provided for each command so that a user can see the definition of all the arguments that the command invokes.
1. First we have to define the model builder. The cantilever column is a 2D model with 3 DOFs at each node. Thus, spatial dimension of the model (NDM) is 2 and number of degrees-of-freedom (ndf) is 3. This is defined in the following way:
model BasicBuilder -ndm 2 -ndf 3
2. The column has two nodes, labeled 1 and 2 (as shown in the Figure above). Node 1 has coordinates (0,0) and node 2 has coordinates (0,432) in the global coordinate system (x,y). The basic units chosen to build the model are: kip, in, sec. Note: y coordinate for node 2 is 36*12=432 in.
Nodes are defined using the node command:
node 1 0. 0. ; node 2 0. 432. ;
3. The cantilever column is constrained (fixed) at the node 1 in all three DOFs (two translational and one rotation). This boundary condition is defined with fix command.
fix 1 1 1 1;
4. Mass is assigned at node 2 using mass command. Since transient analysis is going to be performed for one component of ground motion (horizontal component - x direction) the mass is to be assigned in x direction. The mass is defined as Weight/g=2000/386=5.18. To be able to solve eigenvalue problem at least two masses have to be assigned to the model. Thereafter, the vertical component of mass will be set to very small value (10^-9). The rotational mass is set to zero.
mass 2 5.18 1.e-9 0.
5. The geometric transformation with id tag 1 is defined to be linear.
geomTransf Linear 1 ;
6. The column is defined to be elastic using elasticBeamColumn element. The element with the id tag 1 will connect nodes 1 and 2. Cross-sectional area of the element is (5*12)*(5*12)=3600in^2, Young's modulus of elasticity is 51000*sqrt(4000)/1000=3225 ksi (assuming fc'=4000 psi), and the moment of inertia is (1/12)*(5*12)^4=1080000 in^4.
element elasticBeamColumn 1 1 2 3600 3225 1080000 1;
Define recorders
As a user you have an option of specifying the type of output that will be created following the analysis. The OpenSees recorder command is used to define the analysis output. This command is used to generate a recorder object for a specific type of response that is to be monitored during the analysis and its output.
For the considered cantilever column, the displacements of free node, support reactions, lateral drift, end element forcesare recorded and stored as text files in "Data" folder.
The node recorder is used to output displacements of the free node (node 2) and support reaction of the constrained node (node 1) into files DFree.out and RBase.out, respectively. Both files will have a time stored in the first column. The columns 2-4 of file DFree.out will contain displacements at DOFs 1, 2, and 3. The columns 2-4 of file RBase.out will contain reactions that correspond to DOFs 1, 2, and 3.
recorder Node -file Data/DFree.out -time -node 2 -dof 1 2 3 disp recorder Node -file Data/RBase.out -time -node 1 -dof 1 2 3 reaction
The drift recorderis used to output lateral drifts into file Drift.out. The first column of the file is the time, and the second column is the lateral drift (relative displacements between nodes 1 and 2).
recorder Drift -file Data/Drift.out -time -iNode 1 -jNode 2 -dof 1 -perpDirn 2
The element recorder is used to output global forces of the column into file FCol.out. The first column of the file is the time. The columns 2-7 of the file will contain end node forces (shear, axial, and bending moment); 3 forces at node 1 and 3 forces at node 2. These forces correspond to the global coordinate axes orientation.
recorder Element -file Data/FCol.out -time -ele 1 force;
Apply gravity load
In this example the gravity load is a substructure weight of 2000 kips. It will be applied at node 2 in 10 equal steps in increments of 200kips (0.1*2000). To apply the nodal load incrementally the linear time series with id tag 1 will be used.
timeSeries Linear 1
The time series will be assigned to the load pattern with id tag 1. Nodal load command will be used to create nodal load. It is a load at node 2 in negative Y direction of 2000 kips. The load value is a reference load value, it is the time series that provides the load factor. The load factor times the reference value is the load that is actually applied to the node.
pattern Plain 1 1 {
load 2 0. -2000. 0.
}
The analysis objects are defined next. To construct Constraint Handler object the constraints command is used. The Constraint Handler object determines how the constraint equations (boundary conditions) are enforced in the analysis. In the case of cantilever column with a total fixity (all DOFs are constrained) at the node 1 plain constraints can be used.
constraints Plain
DOF_Numberer object, that determines the numbering of degrees of freedom (mapping between equation numbers and degrees-of-freedom) is defined next. Since the model is very simple and small plain numberer will be used:
numberer Plain
To store and solve the system of equations during the analysis BandGeneral solver is used:
system BandGeneral
Since the column is elastic the system of equation can be solved in one iteration. Thus, the linear algorithm will be used to solve the system of equations.
algorithm Linear
Since the analysis is static and specific load (2000 kips) is to be applied, load controlintegrator will be used in this example. The load factor increment (<math>\delta \lambda</math>) is set to 0.1 since we want to apply the full load in 10 analysis steps. For the nth step of analysis the load factor will be:<math>\lambda_{n}=\lambda_{n-1}+\delta \lambda</math>.