Eigen analysis of a two-story shear frame

Example Provided by: Vesna Terzic, UC Berkeley

---

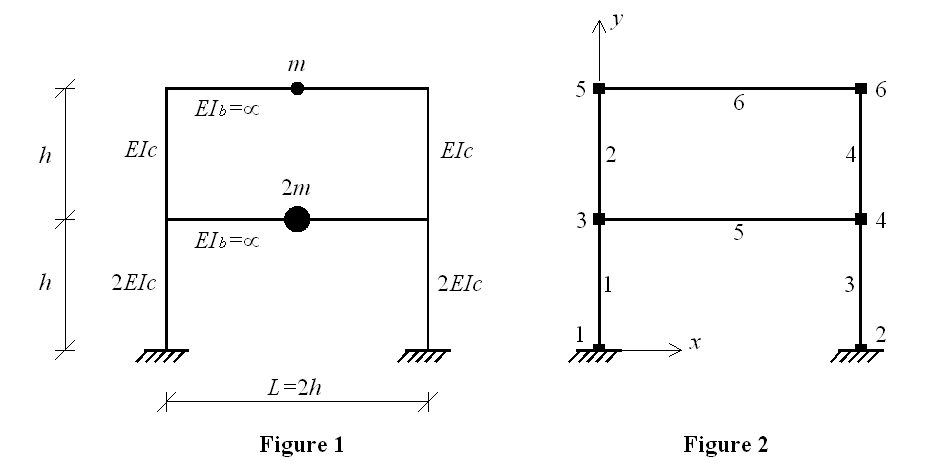
This example demonstrates how to perform eigenvalue analysis and plot mode shapes. Two-storey shear frame (Example 9.1a from "Dynamic of Structures" book by Professor Anil K. Chopra) is used for this purpose. Geometry and material characteristics of the frame structure are shown in Figure 1. Node and element numbering is given in Figure 2.

Instructions on how to run this example

To execute this ananlysis in OpenSees download this file: EigenAnal_twoStoreyShearFrame.tcl

To run this example, place the OpenSees.exe to the same directory with the downloaded file. By double cliking on OpenSees.exe the OpenSees interpreter will pop out. To run the analysis the user sholud type "source EigenAnal_twoStoreyShearFrame2-1.tcl" in OpenSees interpreter and hit enter. To create output files of eigenvectors (stored in directory "modes") the user has to exit OpenSees interpreter by typing "exit".

equalDOF

Create the model

Spatial dimension of the model and number of degrees-of-freedom (DOF) at nodes are defined using model command. In this example we have 2D model with 3 DOFs at each node. This is defined in the following way:

model BasicBuilder -ndm 2 -ndf 3

Nodes of the structure (Figure 2) are defined using the node command:

node 1   0.  0. ;
node 2   $L  0. ;
node 3   0.  $h ;
node 4   $L  $h ;
node 5   0.  [expr 2*$h];
node 6   $L  [expr 2*$h];

The boundary conditions are defined next using single-point constraint command fix. In this example nodes 1 and 2 are fully fixed at all three DOFs:

fix 1 1 1 1;
fix 2 1 1 1;

Masses are assigned at nodes 3, 4, 5, and 6 using mass command. Since the considered shear frame system has only two degrees of freedom (displacements in x at the 1st and the 2nd storey), the masses have to be assigned in x direction only.

mass 3 $Mass 0. 0. ;
mass 4 $Mass 0. 0. ;
mass 5 [expr $Mass/2.] 0. 0. ;
mass 6 [expr $Mass/2.] 0. 0. ;

The geometric transformation with id tag 1 is defined to be linear.

set TransfTag 1;
geomTransf Linear $TransfTag ;

In this example, for the sake of simplicity the beams and columns of the frame are defined to be elastic using elasticBeamColumn element.

element elasticBeamColumn 1 1 3 $Ac $Ec [expr 2.*$Ic] $TransfTag;
element elasticBeamColumn 2 3 5 $Ac $Ec $Ic           $TransfTag;
element elasticBeamColumn 3 2 4 $Ac $Ec [expr 2.*$Ic] $TransfTag;
element elasticBeamColumn 4 4 6 $Ac $Ec $Ic           $TransfTag;
element elasticBeamColumn 5 3 4 $Ac $Eb $Ic           $TransfTag;
element elasticBeamColumn 6 5 6 $Ac $Eb $Ic           $TransfTag;

In order to make beams infinitely rigid modulus of elasticity for beams (Eb) is set to very high value (10e+12). To comply with the assumptions of shear frame (no vertical displacemnts and rotations at nodes) end nodes of the beams are constrained to each other in the 2nd DOF (vertical displacement) and the 3rd DOF (rotation). EqualDOF command is used to imply these constraints.

equalDOF 3 4 2 3
equalDOF 5 6 2 3