Flexure-Shear Interaction Displacement-Based Beam-Column Element

From OpenSeesWiki
Revision as of 00:10, 25 March 2010 by Fmk (talk | contribs)
Jump to navigation Jump to search



This command is used to construct a dispBeamColumnInt element object, which is a distributed-plasticity, displacement-based beam-column element which includes interaction between flexural and shear components.


element dispBeamColumnInt $eleTag $iNode $jNode $numIntgrPts $secTag $transfTag $cRot <-mass $massDens>



$eleTag unique element object tag
$iNode $jNode end nodes
$numIntgrPts number of integration points along the element.
$secTag identifier for previously-defined section object
$transfTag identifier for previously-defined coordinate-transformation (CrdTransf) object
$cRot identifier for element center of rotation. Fraction of the height distance from bottom to the center of rotation (0 to 1)
$massDens element mass density (per unit length), from which a lumped-mass matrix is formed (optional, default=0.0)


NOTE:

  1. The valid queries to a nonlinear beam-column element when creating an ElementRecorder object are 'force,' and 'section $secNum secArg1 secArg2...' Where $secNum refers to the integration point whose data is to be output.
  2. The element requires a special section and special care when numbering the materials. see Discussion below for section command and material numbering.

EXAMPLE:

geomTransf LinearInt 1

element dispBeamColumnInt 1 1 3 2 2 1 0.4


DISCUSSION:

In the original fiber element (Displacement-Based Beam-Column Element) implemented in OpenSees, based on linear interpolation of the curvature and constant axial strain, a third strain component was included to account for shear flexibility. The fiber discretization leads no longer to just uniaxial behavior, but rather a biaxial response by incorporating a membrane material model based on simple uniaxial stress-strain curves for concrete and steel. Although the material models can be cyclic, the element model formulation has been implemented and verified initially for monotonic static analysis. Details of the formulation can be found elsewhere (Massone et al., 2006; Massone 2006). The compatibility equations to relate nodal displacements (6 DOF) and internal strains (axial strain, curvature and shear strain) are defined only in a 2D plane, so that no 3D analysis is possible with this element. It also requires a specific geometric transformation called "LinearInt", which is based on the traditional geometric linear transformation, and therefore no other geometric transformation can be used.

The input parameters are the same as the original fiber element, however a new term, the location of the center of rotation (c), is required to distribute transversal displacement between flexural (curvature) and shear (shear strain) components. This parameter is defined as the fraction of the element height (measured from top) that corresponds to the center of curvature.

The section formulation required for each element is based also on a similar formulation implemented in OpenSees. However, not all capabilities are included as in the original formulation. The section is defined as a fiber section, but based only in fiber components and not in patch or layer components for simplicity. It has been formulated in this way to make sure that the strip modeling is understood since differently to the standard fiber section analysis the strips in the model with interaction between shear and flexure requires that all the strips are formed with smeared (average) concrete and reinforcement areas.

SECTIONAL ANALYSIS

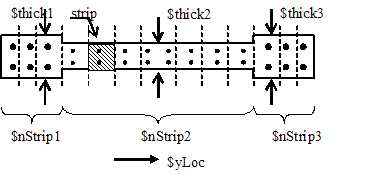
The definition of the fiber section is initiated by establishing in the heading of the command the thickness of the section (three in this case to represent boundary elements). The thickness of the element is required to verify equilibrium in the horizontal direction (assuming that same area ratio holds between concrete materials inside a strip in horizontal and vertical directions). For generality, the section is allowed to have three different thicknesses to be able to model barbell or T-shaped walls (Fig. 1). Each thickness may be associated to several strips.

Strips are created from concrete and steel materials. Since the strip unit corresponds to the membrane (panel) element, the location of each of them is defined by the fiber coordinate ($yLoc), and therefore, tributary concrete and steel areas inside each strip are located at one same point (Fig. 1). This may difficult the analysis, but the model is based on uniform (smeared) steel and concrete distribution. Even though a center of area (concrete and steel) defined by using a transformed area for steel may be acceptable, in tensile governed elements a better approximation may be using the steel location. For simplicity, the center of area of concrete may be selected for calculations, regarding a reasonable small strip size selection. In the fiber section definition, each strip is defined by fibers with same coordinate, and strips are organized from negative to positive location. Therefore all steel and concrete components of one strip have to be together (one after the other). The change in fiber location tells the program that a different strip is initiated. To complete the strip definition, the horizontal steel reinforcement has to be included. The steel is assumed uniformly distributed in the section, so that it may be located as only one fiber (recommended). In the case of horizontal steel, the component is called as "Hfiber" and the area defined in such fiber corresponds to the total horizontal steel area in one single element (for the entire element). This steel is assumed to be the same for all strips inside the section.

For consistency when defining the fiber section, the command requires to define the number of strips within each sub-section with the same thickness, which has to add up the same number of different fiber locations defined in the section (total number of strips).

The original uniaxial definition of the fiber components inside the fiber section recorded only uniaxial stresses and strains for the fiber, and resultant axial force, moment, axial strain and curvature for the section. In the membrane (panel) formulation for the strips, other quantities may be useful to record. At the strip level new recorders have been included: eX (horizontal strain), eY (axial strain), e1 (principal strain in direction 1), e2 (principal strain in direction 2), alpha (angle for principal axis, measured counterclockwise from eY to e1), sX (average horizontal steel stress), sY (average vertical steel stress), s1 (average principal concrete stress in direction 1) and s2 (average principal concrete stress in direction 2). The mentioned recorders are called by sections, so that the output gives the results organized in columns for each strip inside the section, using the same order defined in the fiber section. At the section level, axial strain, curvature, shear strain, resultant axial force, moment and shear force are obtained with the standard recorder forceAndDeformation.

Example:

recorder Element -file Sect_eX.out -ele 1 section 1 eX

recorder Element -file Sect_s2.out -ele 1 section 1 s2


This commnand allows the user to construct a FiberSection object. Each FiberSection object is composed of Fibers, with each fiber containing a UniaxialMaterial, an area and a location (y,z). The command to generate FiberSection object contains in { } the commands to generate all the fibers in the object. To construct a FiberSection and populate it, the following command is used:

section FiberInt $secTag -NStrip $nStrip1 $thick1 $nStrip2 $thick2 $nStrip3 $thick3 {
fiber...
Hfiber ...
...
}


$sectTag unique tag among FiberSections
$thick1 section thickness 1.
$nStrip1' number of strips with thickness $thick1. Considers first $nStrip1 strips in the fiber section with thickness $thick1.
$thick2 section thickness 2.
$nStrip2' number of strips with thickness $thick2. Considers next $nStrip2 strips in the fiber section with thickness $thick2.
$thick3 section thickness 3.
$nStrip3' umber of strips with thickness $thick3. Considers last $nStrip3 strips in the fiber section with thickness $thick3. Total number of strips has to match the fiber section defined.
fiber... command to generate cncrete and vertical steel fibers.
Hfiber... command to generate horizontal steel fibers
'...

EXAMPLE:

Example:

section FiberInt 2 –NStrip 1 6.5 1 2.0 1 6.5 {

fiber -25.55 0 15.6 2

fiber -25.55 0 1.24 1003

fiber 0 0 35.6 2

fiber 0 0 0.84 1003

fiber +25.55 0 15.6 2

fiber +25.55 0 1.24 1003

Hfiber 0 0 0.0718 1005

}


FIBER MODELLING:

As described previously, the section is created based on strips, and each strip consists of vertical fibers (fiber) that represent steel and concrete materials and horizontal fibers (Hfiber) that represent the horizontal steel. Since uniform distribution of reinforcement steel is assumed at strip level, all horizontal steel reinforcement can be included as only one horizontal fiber. The location of such fiber is included in the command just for completeness, but it is not necessary for any calculation. The area required in the Hfiber corresponds to the total steel tributary area present in the element that holds the defined section. The internal numerical scheme defined to achieve equilibrium handles two different types of materials: steel and concrete. Since different steel and concrete stress-strain laws can be implemented and used with this model, the program needs to distinguish between concrete and steel. For simplicity, it has been selected the material tag ($matTag) to define whether a material is concrete or steel. Concrete materials are defined as materials with tag number under (or equal to) 1000 and steel materials use tag numbers over 1000 (see example).

HFiber Command

Hfiber $yLoc $zLoc $A $matTag



$yLoc y coordinate of the fiber in the section (just for completeness, not required in calculations)
$zLoc z coordinate of the fiber in the section (just for completeness, not required in calculations)
$A total steel area located inside the section
$matTag identifier for previously-defined material object


Example:

uniaxialMaterial Concrete01 2 -3 -0.002 0 -0.01

uniaxialMaterial Steel02 1003 60 29000 0.02 20 0.9 0.2 0 0.1 0 0.1

uniaxialMaterial Steel02 1005 60 29000 0.02 20 0.9 0.2 0 0.1 0 0.1

.

.

.

fiber -25.55 0 15.6 2 # vert. concrete

fiber -25.55 0 1.24 1003 # vert. steel

Hfiber 0 0 0.0718 1005 # horz. steel

NOTE Note: concrete materials are defined as materials with tag number under (or equal) 1000 and steel materials use tag numbers over 1000 (see example).



REFERENCES:

1. Massone, L. M., 2006; "RC Wall Shear – Flexure Interaction: Analytical and Experimental Responses", Ph.D. Dissertation, University of California, Los Angeles, June 2006, 398 pp.

2. Massone, L. M.; Orakcal, K.; and Wallace, J. W. , 2006; "Shear - Flexure Interaction for Structural Walls"; SP-236, ACI Special Publication – Deformation Capacity and Shear Strength of Reinforced Concrete Members Under Cyclic Loading, editors: Adolfo Matamoros & Kenneth Elwood, p. 127-150.



Code Developed by: Leo Massone, University of Chile and Kutay Orakcal and John Wallace, UCLA

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=Flexure-Shear_Interaction_Displacement-Based_Beam-Column_Element&oldid=3120"