ZeroLengthContactNTS2D
This command is used to construct a zeroLengthContactNTS2D element object. This is a Node-To-Segment (NTS) frictional contact element used in two dimensional analysis for contact between elements with 2 DOF nodes.
| element zeroLengtContactNTS2Dh $eleTag -sNdNum $sNdNum -mNdNum $mNdNum -Nodes $Nodes $Kn $kt $phi |
| $eleTag | unique element object tag |
| $sNdNum | Number of Slave Nodes |
| $mNdNum | Number of Master nodes |
| $Nodes ... | Slave and master node tags respectively |
| $Kn | Penalty in normal direction |
| $Kt | Penalty in tangential direction |
| $phi | Friction angle in degrees |
NOTES:
- The contact element is node-to-segment (NTS) contact. The relation follows Mohr-Coulomb frictional law: <math>T = N tan(\phi)</math>, where T is the tangential force, N is normal force across the interface and ,math>\phi</math> is friction angle.
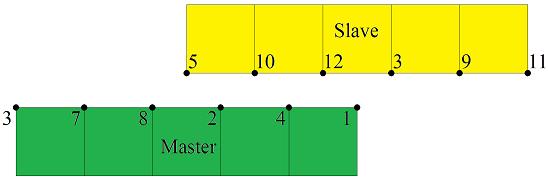
- For 2D contact, slave nodes and master nodes must be 2 DOF and notice that the slave and master nodes must be entered in counterclockwise order.
- The resulting tangent from the contact element is non-symmetric. Switch to the non-symmetric matrix solver if convergence problem is experienced.
- As opposed to node-to-node contact, predefined normal vector for node-to-segment (NTS) element is not required because contact normal will be calculated automatically at each step.
- contact element is implemented to handle large deformations.
EXAMPLE:
element zeroLengthContactNTS2D 1 -sNdNum 6 -mNdNum 6 - Nodes 5 10 12 3 9 11 1 4 2 8 7 1e8 1e8 16
Example 1:
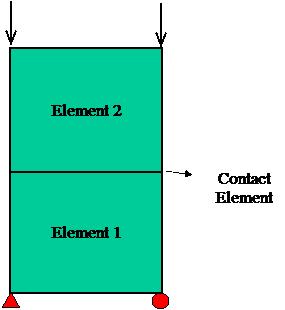
This example simply shows the two quadrilateral elements in normal contact. The top element is in normal downward uniform force. The Tcl script of this example can be found File:ZeroLengthContactNTS2D Example1.tcl.
Example 2:
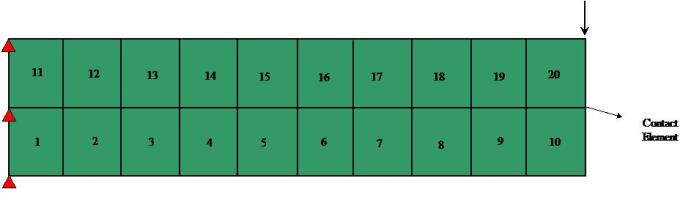
This example shows two cantilever beams in contact. The beams were modeled using four-node quadrilateral elements and the end of top beam was subjected to a linearly increasing displacement. The Tcl scripts for this example can be found here.
The following Figure shows the deflections of the two beams.
REFERENCES:
- P. Wriggers, V.T. Vu and E. Stein, Finite-element formulation of large deformation impact–contact problems with friction, Comput. Struct. 37 (1990), pp. 319–331.
- Peter Wriggers. Computational Contact Mechanics. John Wiley & Sons Ltd. Chichester, 2002.
Code Developed by: Roozbeh G. Mikola, UC Berkeley and N. Sitar, UC Berkeley