LeadRubberX

This command is used to construct a LeadRubberX bearing element object in three-dimension. The 3D continuum geometry of a lead rubber bearing is modeled as a 2-node, 12 DOF discrete element. It extends the formulation of ElastomericX by including strength degradation in lead rubber bearing due to heating of lead-core. The LeadRubberX element requires only the geometric and material properties of an elastomeric bearing as arguments. The material models in six direction are formulated within the element from input arguments. The time-dependent values of mechanical properties (e.g., shear stiffness, buckling load capacity, temperature in the lead core, yield strength) can also be recorded using the "parameters" recorder.

For a 3D problem:

element LeadRubberX $eleTag $Nd1 $Nd2 $qLead $uh $Gr $Kbulk $D1 $D2 $ts $tr $n <<$x1 $x2 $x3> $y1 $y2 $y3> <$kc> <$PhiM> <$ac> <$sDratio> <$m> <$cd> <$tc> <$qL> <$cL> <$kS> <$aS> <$tag1> <$tag2> <$tag3> <$tag4> <$tag5>

---

$eleTag	unique element object tag
$Nd1 $Nd2	end nodes
$qLead	yield strength
$uh	yield deformation
$Gr	shear modulus of elastomeric bearing
$Kbulk	bulk modulus of rubber
$D1	internal diameter
$D2	outer diameter (excluding cover thickness)
$ts	single steel shim layer thickness
$tr	single rubber layer thickness
$n	number of rubber layers
$x1 $x2 $x3	vector components in global coordinates defining local x-axis (optional)
$y1 $y2 $y3	vector components in global coordinates defining local y-axis (optional)
$kc	cavitation parameter (optional, default = 10.0)
$PhiM	damage parameter (optional, default = 0.5)
$ac	strength reduction parameter (optional, default = 1.0)
$sDratio	shear distance from iNode as a fraction of the element length (optional, default = 0.5)
$m	element mass (optional, default = 0.0)
$cd	viscous damping parameter (optional, default = 0.0)
$tc	cover thickness (optional, default = 0.0)
$qL	density of lead (optional, default = 11200 kg/m3)
$cL	specific head of lead (optional, default = 130 N-m/kg oC)
$kS	thermal conductivity of steel (optional, default = 50 W/m oC)
$aS	thermal diffusivity of steel (optional, default = 1.41e-05 m2/s)
$tag1	Tag to include cavitation and post-cavitation (optional, default = 0)
$tag2	Tag to include buckling load variation (optional, default = 0)
$tag3	Tag to include horizontal stiffness variation (optional, default = 0)
$tag4	Tag to include vertical stiffness variation (optional, default = 0)
$tag5	Tag to include strength degradation in shear due to heating of lead core (optional, default = 0)

Important note:

Because default values of heating parameters are in SI units, user must override the default heating parameters values if using Imperial units

Physical Model and Mechanical Properties

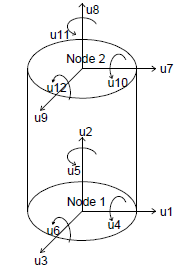
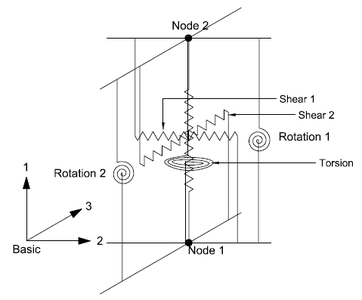
The physical model of an elastomeric bearing is considered as a two-node, twelve degrees-of-freedom discrete element. The two nodes are connected by six springs that represent the mechanical behavior in the six basic directions of a bearing. The degrees of freedom and discrete spring representation of an elastomeric bearing are shown in the below figures.

The general form of element force vector, <math>{{f}_{b}}</math>, and element stiffness matrix,<math>{{K}_{b}}</math> , for element representation considered above is given by equation below:

<math>{{f}_{b}}=\left[ \begin{matrix}

  Axial  \\
  Shear1  \\
  Shear2  \\
  Torsion  \\
  Rotation1  \\
  Rotation2  \\

\end{matrix} \right];\ \ \ \ \ \ {{K}_{b}}=\left[ \begin{matrix}

  Axial & 0 & 0 & 0 & 0 & 0  \\
  0 & Shear1 & Shear12 & 0 & 0 & 0  \\
  0 & Shear21 & Shear2 & 0 & 0 & 0  \\
  0 & 0 & 0 & Torsion & 0 & 0  \\
  0 & 0 & 0 & 0 & Rotation1 & 0  \\
  0 & 0 & 0 & 0 & 0 & Rotation2  \\

\end{matrix} \right]</math>

The coupling of the two shear springs is considered directly by using a coupled bidirectional model. All other springs are uncoupled. The coupling of vertical and horizontal directions are considered indirectly by using expressions for mechanical properties in one direction that are dependent on the response parameters in the other direction. Linear uncoupled springs are considered in the torsion and the two rotational springs as they are not expected to significantly affect the response of an elastomeric bearing. The off-diagonal terms due to coupling between axial and shear, and axial and rotation, are not considered in the two-spring model (Koh and Kelly, 1987) used here. An exact model would have non-zero values of these off-diagonal terms. A discussion on the formulation of the two-spring model and the exact model is presented in Ryan et al.(1991). The subscript b refers to the element’s basic coordinate system. When the model is implemented in software programs, response quantities are transformed between the basic, local and global coordinates to perform computations.

The discrete spring model presented here has the advantages of easy implementation and being computationally efficient. The mechanical properties of the six springs (also referred to as material models in OpenSees) are defined using analytical solutions available from the analysis of elastomeric bearings. The expression for mechanical properties, including stiffness and buckling load capacity, are derived using explicit consideration for geometric nonlinearity due to large displacement effects. The P-Delta effect, which is an approximate method to account for geometric nonlinearity in structural analysis problems, is therefore not considered. The material models in six directions are:

• Axial direction: a new mathematical model that captures the behavior under cyclic tension Link
• Two shear directions: a special case of the Bouc-Wen model extended by Nagarajaiah et al.(1991) for seismic isolation bearings combined with a strength degradation model of Kalpakidis et al.(2010)
• Torsion: a linear elastic model
• Two rotational directions: linear elastic models

In addition to the behavior captured by existing bearing elements, this element can capture following characteristics:

1. Cavitation and post-cavitation behavior in tension (tag1)
2. Variation in critical buckling load capacity due to lateral displacement (tag2)
3. Variation in horizontal shear stiffness with axial load on the bearing (tag3)
4. Variation in vertical axial stiffness with horizontal displacement (tag4)
5. Strength degradation in cyclic shear loading due to heating of lead core (tag5)

User may choose to include an individual or a combination of these behaviors through user tags (include:1, exclude:0) in their analysis.

For the full capabilities of this element, users are referred to: EESD Article

Consideration of characteristics to include under extreme loading

A recent paper by Kumar et. al (2015) explains which of the five tags should be included in the analysis. Although the analysis presented in the paper is for the base-isolated NPP, the conclusions are valid for design earthquake and maximum considered earthquake for regular building structures as well. Following are few thumb rules that can be followed: tag 1: Unless you are investigating the tensile behavior, the effect of the tensile model on shear response is insignificant. tag 2: It is recommended to use tag to include variable buckling load capacity. It affects the compression capacity and shear stiffness. The apparent softening in shear force-deformation behavior at high axial load is due to this. A constant buckling load will show less softening. tag 3: Recommended if axial load expected during the loading is more than 10% of the buckling load capacity. tag2+tag3 provides greater softening. tag 4: Unless you are investigating the axial behavior, the effect of the tensile model on shear response is insignificant. tag 5: Recommended for long duration and low frequency ground motions. Effect is more prominent at beyond design basis earthquakes.

Verification and validation

This is element has been verified per ASME guidelines. Users are referred to the SMiRT23 Paper and chapter 4 of the Manish Kumar's Dissertation for complete details.

Recorders

In addition to regular recorders provided by the bearing elements ( Element Recorder), this element can also record instantaneous values of cavitation force (Fcn), buckling load capacity (Fcrn), vertical stiffness (Kv), horizontal stiffness (ke), temperature increase (dT), and yield strength (qYield) using the "Parameters" recorder in that order.

        Example: recorder Element <-file $fileName> -time <-ele ($ele1 $ele2 ...)> Parameters
        recorder Element -file param.out -time -ele 1 Parameters

To check if bearing has buckled or cavitated, an user can obtain the histories of Fcn and Fcrn as described above and divide the axial force (obtained from basicForce recorder, qb(2)) by Fcn and Fcrn at each time step, which provides demand vs capacity (D/C) ratios at each time step. If Fcn/qb(0) > 1.0 : Cavitation, or Fcrn/qb(0)>1.0 : Buckling.

Examples

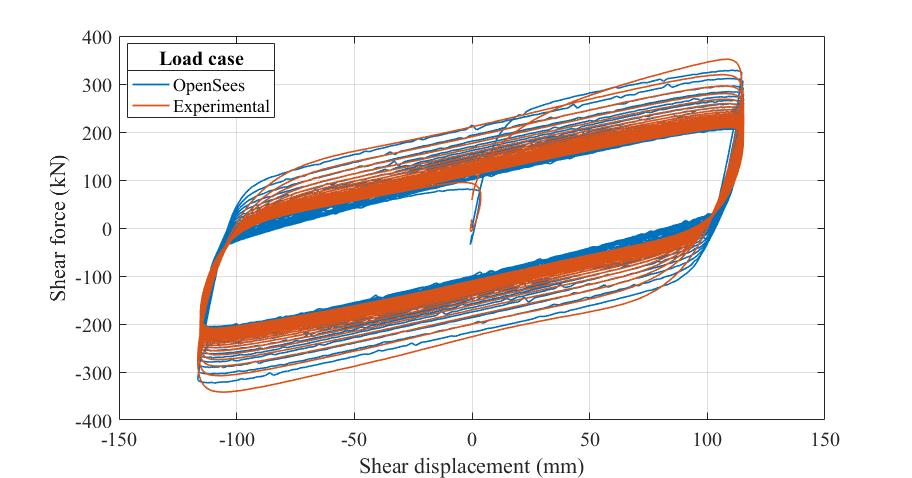
An example is presented here in which a lead rubber bearing (large size bearing in Kalpakidis et al. (2010)) is subjected to a shear harmonic loading in laboratory (SEESL at UB). The response obtained from LeadRubberX element in OpenSees is compared with the experimental results.

Excitation files: File:Excitation.zip ‎

Tcl files: File:LDRgravity.tcl File:LDRtest.tcl

References

1. Kumar, M., Whittaker, A., and Constantinou, M. (2014). "An advanced numerical model of elastomeric seismic isolation bearings." Earthquake Engineering & Structural Dynamics, 43(13), 1955-1974. Link
2. Kumar, M., Whittaker, A., and Constantinou, M. (2015). "Experimental investigation of cavitation in elastomeric seismic isolation bearings." Engineering Structures, 101, 290-305. Link
3. Kumar, M., Whittaker, A., and Constantinou, M. (2015). "Response of base-isolated nuclear structures to extreme earthquake shaking." Nuclear Engineering and Design (In press). Link
4. Kalpakidis, I. V., Constantinou, M. C., and Whittaker, A. S. (2010). "Modeling strength degradation in lead-rubber bearings under earthquake shaking." Earthquake Engineering and Structural Dynamics, 39(13), 1533-1549.

---

Code Developed by: Manish Kumar, University at Buffalo, SUNY.

Any bugs in this element can be reported to mkumar2 AT buffalo dot edu