Maxwell Material

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

This command is used to construct a ViscousDamper material, which represents the Maxwell Model (linear spring and nonlinear dashpot in series). The Maxwell material simulates the hysteretic response of viscous dampers.

uniaxialMaterial ViscousDamper $matTag $K $Cd $alpha

---

$matTag	integer tag identifying material
$K	Elastic stiffness of linear spring (to model the axial flexibility of a viscous damper (brace and damper portion)
$Cd	Viscous parameter of damper
$alpha	Viscous damper exponent

---

Examples:

1. Input parameters:

Assume a viscous damper with axial stiffness K=300.0kN/mm, viscous parameter Cd=280.3kN(s/mm)0.3, and exponent a=0.30.

The input parameters for the material should be as follows:

uniaxialMaterial ViscousDamper 1 300 280.3 0.30

Using these properties, Figure 1 shows the hysteretic response of this damper for sinusoidal displacement increments of 12, 24 and 36mm and a frequency f = 0.5Hz.

The sensitivity of the viscous damper with respect to its axial stiffness is shown in Figures 2 to 5 for the following set of parameters:

Figure 1. Viscous Damper with K=300.0 kN/mm, Cd=73.0kN(s/mm)0.6, a=0.60 , Figure 2. Viscous Damper with K=300.0 kN/mm, Cd=12.0kN(s/mm)1.0, a=1.0

Figure 2. Viscous Damper with K=300.0 kN/mm, Cd=683.0kN(s/mm)0.1, a=0.1 , Figure 2. Viscous Damper with K=300.0 kN/mm, Cd=1017.7kN(s/mm)0.01, a=0.01

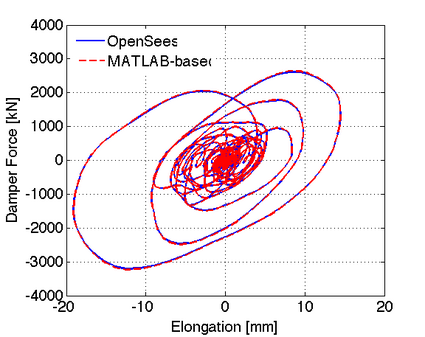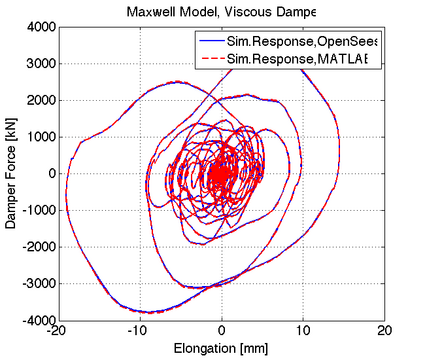2. Tcl input file for Viscous Damper Calibration.

3. OpenSees Example of 1-story steel moment frame with a viscous damper: (to be posted)

---

References:

[1]	Olsson, A.K., and Austrell, P-E., (2001), "A fitting procedure for viscoelastic-elastoplastic material models," Proceedings of the Second European Conference on Constitutive Models for Rubber, Germany, 2001.
[2]	Ottosen, N.S., and Ristinmaa, M., (1999). "The mechanics of constitutive modelling, (Numerical and thermodynamical topics)," Lund University,Division of Solid Mechanics, Sweden, 1999.

Code Developed by : Prof. Kazuhiko Kasai and implemented by Sarven Akcelyan & Prof. Dimitrios G. Lignos, (McGill University)