PressureDependMultiYield02-Example 2

Command_Manual
- Tcl Commands
- Modeling_Commands
  - model
  - uniaxialMaterial
  - ndMaterial
  - frictionModel
  - section
  - geometricTransf
  - element
  - node
  - sp commands
    - fix
    - fixX
    - fixY
    - fixZ
  - mp commands
  - timeSeries
  - pattern
  - mass
  - block commands
    - block2D
    - block3D
  - region
  - rayleigh
- Analysis Commands
- Output Commands
  - recorder
  - record
  - print
  - printA
  - logFile
  - RealTime_Output_Commands
- Misc Commands
- DataBase Commands
  - Template:DataBaseCommandsMenu

Solid-fluid fully coupled (u-p) 8-node brick element: saturated soil element with pressure dependent material, subjected to 1D sinusoidal base shaking

Input File

# single BrickUP element with pressure dependent material.
# subjected to 1D sinusoidal base shaking 

# Written by Jinchi Lu and Zhaohui Yang (May 2004)

wipe
set friction 31.           ;#friction angle
set phaseTransform 26.     ;#phase transformation angle
set G1 9.e4  ;
set B1 22.e4 ;
set gamma    0.600      ;# Newmark integration parameter

set dt   0.01           ;# time step for analysis, does not have to be the same as accDt.
set numSteps 2500       ;# number of time steps
set rhoS  1.80          ;# saturated mass density
set rhoF  1.00          ;# fluid mass density

set Bfluid 2.2e6        ;# fluid shear modulus
set perm   1.e-5    ;#permeability (m/s)
set accGravity 9.81  ;#acceleration of gravity
set perm   [expr $perm/$accGravity/$rhoF]    ;# actual value used in computation
set matTag 1            ;# material tag

set accMul 1                    ;# acceleration multiplier 
set pi 3.1415926535                     ;
set inclination 0;

set massProportionalDamping   0.0 ;
set InitStiffnessProportionalDamping 0.002;

set gravityX [expr $accGravity*sin($inclination/180.0*$pi)] ;# gravity acceleration in X direction
set gravityY 0.0                                        ;# gravity acceleration in Y direction
set gravityZ [expr -$accGravity*cos($inclination/180.0*$pi)]  ;# gravity acceleration in Z direction

set ndm    3            ;# space dimension

model BasicBuilder -ndm $ndm -ndf 4

nDMaterial PressureDependMultiYield02 $matTag $ndm $rhoS $G1 $B1  $friction 0.1 80 0.5 \
                                      $phaseTransform 0.067 0.23 0.06 0.27

node        1      0.00000     0.0000    0.00000
node        2      0.00000     0.0000    1.00000
node        3      0.00000     1.0000    0.00000
node        4      0.00000     1.0000    1.00000
node        5      1.00000     0.0000    0.00000
node        6      1.00000     0.0000    1.00000
node        7      1.00000     1.0000    0.00000
node        8      1.00000     1.0000    1.00000

element brickUP   1      1    5    7    3     2    6    8    4  $matTag $Bfluid $rhoF $perm $perm $perm $gravityX $gravityY $gravityZ 

updateMaterialStage -material $matTag -stage 0

fix      1      1      1      1   0
fix      2      0      1      0   1
fix      3      1      1      1   0
fix      4      0      1      0   1
fix      5      1      1      1   0
fix      6      0      1      0   1
fix      7      1      1      1   0
fix      8      0      1      0   1


# equalDOF
# tied nodes around
equalDOF      2     4  1      3
equalDOF      2     6  1      3
equalDOF      2     8  1      3


set nodeList {}
for {set i 1} {$i <=   8 } {incr i 1} {
   lappend nodeList $i
}

set elementList {}
for {set i 1} {$i <=   1 } {incr i 1} {
   lappend elementList $i
}

# GRAVITY APPLICATION (elastic behavior)
# create the SOE, ConstraintHandler, Integrator, Algorithm and Numberer
numberer Plain
system ProfileSPD
test NormDispIncr 1.0e-8 20 1
algorithm KrylovNewton
constraints Penalty 1.e18 1.e18
set nw 1.5
integrator Newmark $nw  [expr pow($nw+0.5, 2)/4] 
analysis Transient 

analyze 10 5.e0

# switch the material to plastic
updateMaterialStage -material $matTag -stage 1

analyze 10 5.e1

setTime 0.0 ;# reset time, otherwise reference time is not zero for time history analysis 
wipeAnalysis

############# create recorders       ##############################
eval "recorder Node -file disp   -time -node $nodeList -dof 1 2 3 -dT 0.01 disp"
eval "recorder Node -file acc  -time -node $nodeList -dof 1 2 3 -dT 0.01 accel"
eval "recorder Node -file pwp  -time -node $nodeList -dof 4 -dT 0.01 vel"
eval "recorder Element -ele $elementList -time -file stress1 -dT 0.01 material 1 stress"
eval "recorder Element -ele $elementList -time -file strain1 -dT 0.01 material 1 strain"
eval "recorder Element -ele $elementList -time -file stress3 -dT 0.01 material 3 stress"
eval "recorder Element -ele $elementList -time -file strain3 -dT 0.01 material 3 strain"
eval "recorder Element -ele $elementList -time -file stress5 -dT 0.01 material 5 stress"
eval "recorder Element -ele $elementList -time -file strain5 -dT 0.01 material 5 strain"

############# create dynamic time history analysis ##################
pattern UniformExcitation 1 1 -accel "Sine 0 10 1 -factor $accMul"
integrator Newmark $gamma  [expr pow($gamma+0.5, 2)/4]  
rayleigh $massProportionalDamping 0.0 $InitStiffnessProportionalDamping 0.0
constraints Penalty 1.e18 1.e18 ;# can't combine with test NormUnbalance   
test NormDispIncr 1.0e-3 25 0   ;# can't combine with constraints Lagrange
#algorithm Newton               ;# tengent is updated at each iteration
algorithm KrylovNewton          ;# 
system ProfileSPD                ;# Use sparse solver. Next numberer is better to be Plain.
numberer Plain                  ;# method to map between between equation numbers of DOFs
analysis VariableTransient      ;# splitting time step requires VariableTransient

############# perform the Analysis and record time used ############# 
set startT [clock seconds]
analyze $numSteps $dt [expr $dt/64] $dt  15
set endT [clock seconds]
puts "Execution time: [expr $endT-$startT] seconds."

MATLAB Plotting File

clear all;

a1=load('acc');
d1=load('disp');
p1=load('pwp');
s1=load('stress1');
e1=load('strain1');
s5=load('stress3');
e5=load('strain3');
s9=load('stress5');
e9=load('strain5');

fs=[0.5, 0.2, 4, 6];
fs2=[0.5, 0.2, 4, 3];
accMul = 2;

%integration point 1 p-q
po=(s1(:,2)+s1(:,3)+s1(:,4))/3;
for i=1:size(s1,1)
    qo(i)=(s1(i,2)-s1(i,3))^2 + (s1(i,3)-s1(i,4))^2 +(s1(i,2)-s1(i,4))^2 + 6.0* (s1(i,5)^2 +s1(i,6)^2+s1(i,7)^2) ;
   qo(i)=sign(s1(i,7))*1/3.0*qo(i)^0.5;
end

figure(1); close 1; figure(1);
%integration point 1 stress-strain
subplot(2,1,1), plot(e1(:,7),s1(:,7),'r');
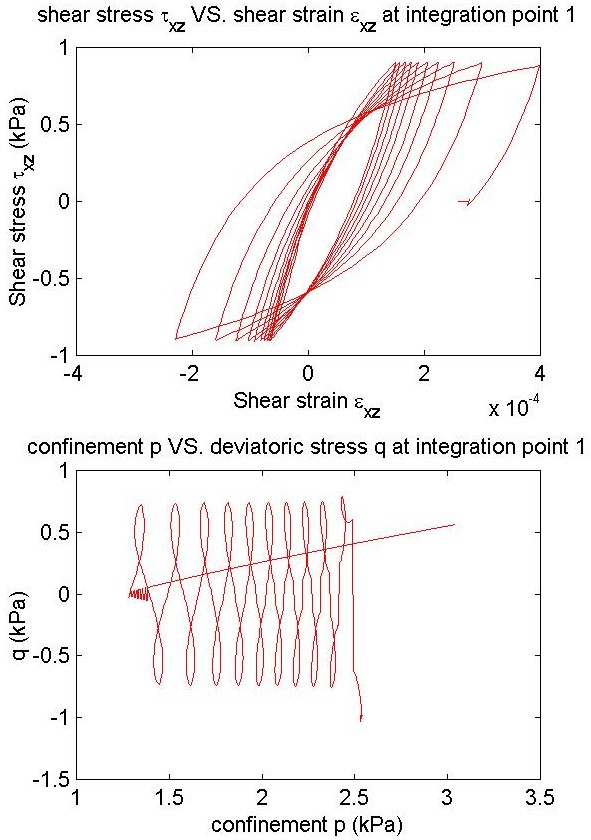
title ('shear stress \tau_x_z VS. shear strain \epsilon_x_z at integration point 1');
xLabel('Shear strain \epsilon_x_z');
yLabel('Shear stress \tau_x_z (kPa)');
subplot(2,1,2), plot(-po,qo,'r');
title ('confinement p VS. deviatoric stress q at integration point 1');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ_p1','jpg');


%integration point 5 p-q
po=(s5(:,2)+s5(:,3)+s5(:,4))/3;
for i=1:size(s5,1)
    qo(i)=(s5(i,2)-s5(i,3))^2 + (s5(i,3)-s5(i,4))^2 +(s5(i,2)-s5(i,4))^2 + 6.0*( s5(i,5)^2 +  s5(i,6)^2 + s5(i,7)^2);
   qo(i)=sign(s5(i,7))*1/3.0*qo(i)^0.5;
end

figure(5); close 5; figure(5);
%integration point 5 stress-strain
subplot(2,1,1), plot(e5(:,7),s5(:,7),'r');
title ('shear stress \tau_x_z VS. shear strain \epsilon_x_z at integration point 3');
xLabel('Shear strain \epsilon_x_z');
yLabel('Shear stress \tau_x_z (kPa)');
subplot(2,1,2), plot(-po,qo,'r');
title ('confinement p VS. deviatoric stress q at integration point 3');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ_p3','jpg');

%integration point 9 p-q
po=(s9(:,2)+s9(:,3)+s9(:,4))/3;
for i=1:size(s1,1)
    qo(i)=(s9(i,2)-s9(i,3))^2 + (s9(i,3)-s9(i,4))^2 +(s9(i,2)-s9(i,4))^2 + 6.0*( s9(i,5)^2 +  s9(i,6)^2 +  s9(i,7)^2);
   qo(i)=sign(s9(i,7))*1/3.0*qo(i)^0.5;
end

figure(6); close 6; figure(6);
%integration point 9 stress-strain
subplot(2,1,1), plot(e9(:,7),s9(:,7),'r');
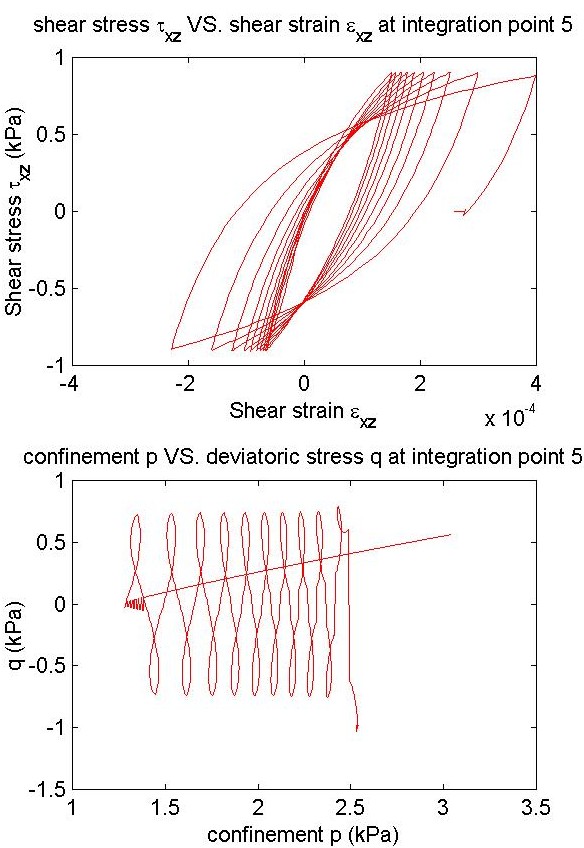
title ('shear stress \tau_x_z VS. shear strain \epsilon_x_z at integration point 5');
xLabel('Shear strain \epsilon_x_z');
yLabel('Shear stress \tau_x_z (kPa)');
subplot(2,1,2), plot(-po,qo,'r');
title ('confinement p VS. deviatoric stress q at integration point 5');
xLabel('confinement p (kPa)');
yLabel('q (kPa)');
set(gcf,'paperposition',fs);
saveas(gcf,'SS_PQ_p5','jpg');

figure(2); close 2; figure(2);
%node 3 displacement relative to node 1
plot(d1(:,1),d1(:,5));
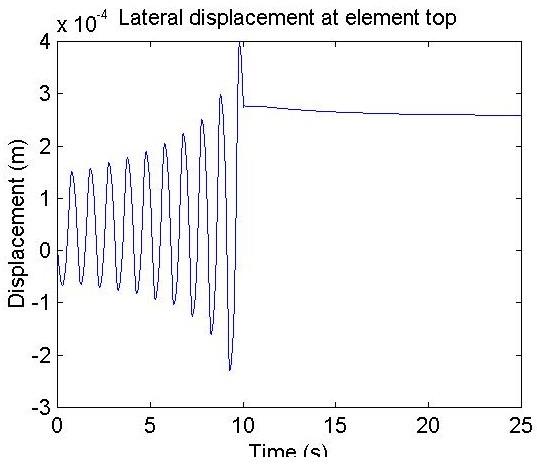
title ('Lateral displacement at element top');
xLabel('Time (s)');
yLabel('Displacement (m)');
set(gcf,'paperposition',fs2);
saveas(gcf,'Disp','jpg');

s=accMul*sin(0:pi/50:20*pi);
s=[s';zeros(3000,1)];
s1=interp1(0:0.01:40,s,a1(:,1));

figure(3); close 3; figure(3);
%node acceleration
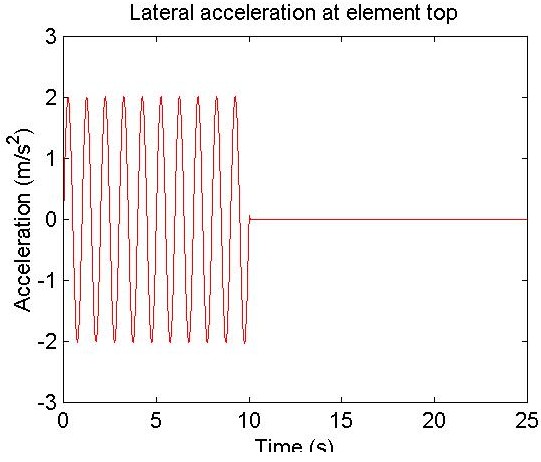
a = plot(a1(:,1),s1+a1(:,5),'r');
title ('Lateral acceleration at element top');
xLabel('Time (s)');
yLabel('Acceleration (m/s^2)');
set(gcf,'paperposition',fs2);
saveas(gcf,'Acc','jpg');

figure(4); close 4; figure(4);
a=plot(p1(:,1),p1(:,2));
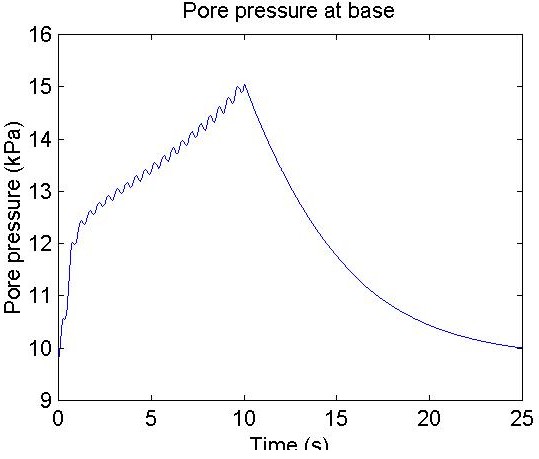
title ('Pore pressure at base');
xLabel('Time (s)');
yLabel('Pore pressure (kPa)');
set(gcf,'paperposition',fs2);
saveas(gcf,'EPWP','jpg');