Elastomeric Bearing (Bouc-Wen) Element

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

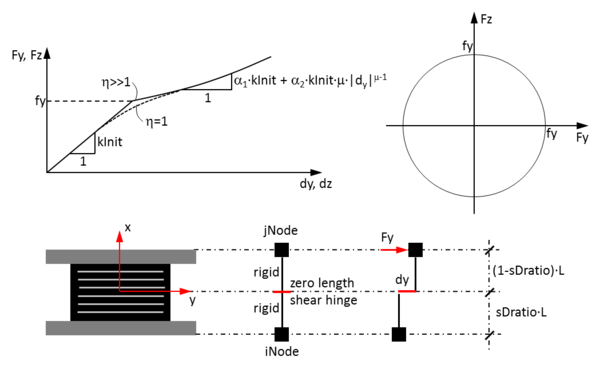
This command is used to construct an elastomericBearing element object, which is defined by two nodes. The element can have zero length or the appropriate bearing height. The bearing has unidirectional (2D) or coupled (3D) plasticity properties for the shear deformations, and force-deformation behaviors defined by UniaxialMaterials in the remaining two (2D) or four (3D) directions. By default (sDratio = 0.5) P-Delta moments are equally distributed to the two end-nodes. To avoid the introduction of artificial viscous damping in the isolation system (sometimes referred to as "damping leakage in the isolation system"), the bearing element does not contribute to the Rayleigh damping by default. If the element has non-zero length, the local x-axis is determined from the nodal geometry unless the optional x-axis vector is specified in which case the nodal geometry is ignored and the user-defined orientation is utilized.

For a two-dimensional problem:

element elastomericBearingBoucWen $eleTag $iNode $jNode $kInit $fy $alpha1 $alpha2 $mu $eta $beta $gamma -P $matTag -Mz $matTag <-orient $x1 $x2 $x3 $y1 $y2 $y3> <-shearDist $sDratio> <-doRayleigh> <-mass $m>

For a three-dimensional problem:

element elastomericBearingBoucWen $eleTag $iNode $jNode $kInit $fy $alpha1 $alpha2 $mu $eta $beat $gamma -P $matTag -T $matTag -My $matTag -Mz $matTag <-orient <$x1 $x2 $x3> $y1 $y2 $y3> <-shearDist $sDratio> <-doRayleigh> <-mass $m>

---

$eleTag	unique element object tag
$iNode $jNode	end nodes
$kInit	initial elastic stiffness in local shear direction
$fy	yield strength
$alpha1	post yield stiffness ratio of linear hardening component
$alpha2	post yield stiffness ratio of non-linear hardening component
$mu	exponent of non-linear hardening component
$eta	yielding exponent (sharpness of hysteresis loop corners) (default = 1.0)
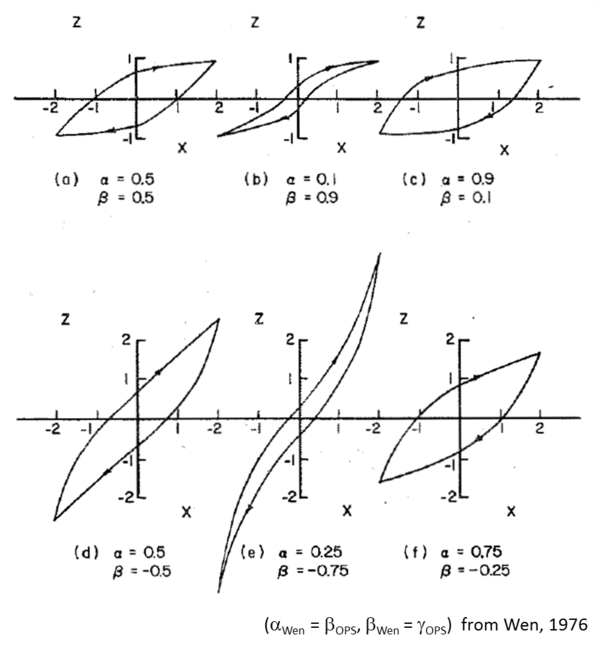
$beta	first hysteretic shape parameter (default = 0.5)
$gamma	second hysteretic shape parameter (default = 0.5)
-P $matTag	tag associated with previously-defined UniaxialMaterial in axial direction
-T $matTag	tag associated with previously-defined UniaxialMaterial in torsional direction
-My $matTag	tag associated with previously-defined UniaxialMaterial in moment direction around local y-axis
-Mz $matTag	tag associated with previously-defined UniaxialMaterial in moment direction around local z-axis
$x1 $x2 $x3	vector components in global coordinates defining local x-axis (optional)
$y1 $y2 $y3	vector components in global coordinates defining local y-axis (optional)
$sDratio	shear distance from iNode as a fraction of the element length (optional, default = 0.5)
-doRayleigh	to include Rayleigh damping from the bearing (optional, default = no Rayleigh damping contribution)
$m	element mass (optional, default = 0.0)

---

NOTE:

1) If the element has zero length and optional orientation vectors are not specified, the local element axes coincide with the global axes. Otherwise the local z-axis is defined by the cross product between the x- and y-vectors specified on the command line.

2) Elastomeric bearings are very stiff in compression, but not rigid. It is not a good idea to specify an extremely large axial stiffness (such as 1E10), because it can lead to problems with numerical sensitivity. Always specify a realistic value for the stiffness of the material that is assigned along the axial direction. To assign different compression and tension stiffness the Elastic or ElasticMultiLinear material can be used.

3) The valid queries to an elastomeric bearing element when creating an ElementRecorder object are 'force,' 'localForce,' 'basicForce,' 'localDisplacement,' 'basicDisplacement' and 'material $matNum matArg1 matArg2 ...' Where $matNum is the number associated with the material whose data is to be output.

---

EXAMPLES:

element elastomericBearingBoucWen 1 1 2 20.0 2.50 0.02 0.0 3.0 1.0 0.5 0.5 -P 1 -Mz 2; # for a 2D elastomeric bearing

element elastomericBearingBoucWen 1 1 2 20 2.50 0.02 0.0 3.0 1.0 0.5 0.5 -P 1 -T 2 -My 3 -Mz 4; # for a 3D elastomeric bearing

---

Code Developed by: Andreas Schellenberg, University of California, Berkeley.