Triple Friction Pendulum Element
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
This command is used to construct a Triple Friction Pendulum Bearing (TPB) (Figure 1) element object. The element is a 3-dimensional element with variable friction coefficient model [1] [2]. The element accounts for the vertical-horizontal coupling and the bidirectional coupling in horizontal behavior. The friction coefficient model is a general model that accounts for the variation of friction coefficient on velocity and vertical force. Other simplified friction coefficient models such as vertical-force-independent friction coefficient, velocity-independent friction coefficient and constant friction coefficient can also be defined. The element can also be used for modeling single friction pendulum bearings or double friction pendulum bearings by simplifying the general backbone curve of the TPB.
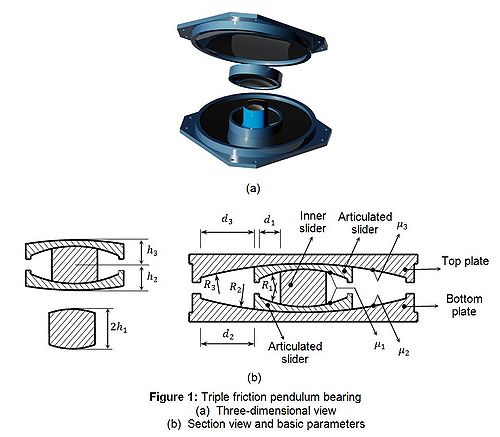
The horizontal normalized behavior of the element is an extension of the unidirectional behavior proposed by Fenz and Constantinou [3] and Morgan and Mahin [4]. The envelope normalized backbone curve for unidirectional behavior is in Figure 2 where effective radii are calculated from L_i=R_i- h_i, based on the bearing geometry in Figure 1. Displacements u_i^* and normalized forces f_i^* are evaluated according to [2], [3] or [4]. The Excel file for generating a backbone curve of a TPB can be downloaded here:Media:TPB_Nhan_BackboneCurve.xls
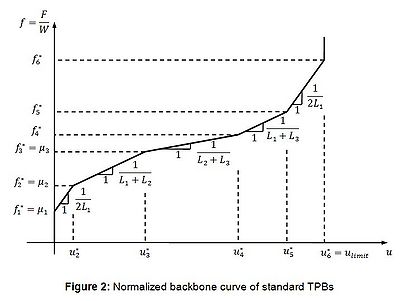
The friction coefficient model μ_i for each contact surface (as identified in Figure 1) is defined as follows:
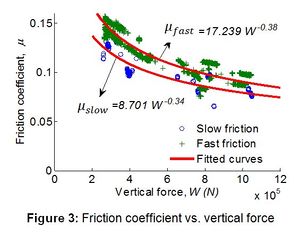
1. Define the friction coefficient at slow (μ_slow) and fast (μ_fast) velocity [5] (Figure 3):
- μ_slow=A_slow.W^(n_slow-1)
- μ_fast=A_fast.W^(n_fast-1)
where A_slow, A_fast, n_slow ≤ 1, n_fast ≤ 1 are constants that determine the friction coefficient models. As the friction coefficients μ_slow and μ_fast are unitless, the user must be careful to define the constants to coincide with the units of the model input data.
2. The friction coefficient as a function of velocity is [6]:
- μ=μ_fast-(μ_fast-μ_slow )exp(-a.udot)
where udot is velocity and a is a rate parameter.
3. In this element, a is assumed to be dependent on vertical force W through:
- a=α_0+α_1.W+α_2.W^2
where α_0, α_1 and α_2 are constants, with units of Time/Length, Time/Length/Force and Time/Length/Force^2 respectively.
Overturning moment and torsion due to the eccentricity of internal forces are equally distributed to the 2 nodes of the element.
In the vertical direction, the element is multi-linear elastic with different stiffnesses k_vc and k_vt in compression and tension, respectively. Even though a TPB has no resistance in tension, a small nonzero stiffness should be provided in tension for stability of the numerical procedure. The reasonable vertical stiffness in tension depends on the stiffness of the superstructure, but a value between 10 N/m to 100 N/m should work well in most cases. Very small ratio of k_vt/k_vc may cause the convergence difficulty when the superstructure is uplifted.
| element TripleFrictionPendulum $eleTag $iNode $jNode $L1 $L2 $L3 $d1 $d2 $d3 $mu1slow $mu1fast $n1slow $n1fast $alpha10 $alpha11 $alpha12 $mu2slow $mu2fast $n2slow $n2fast $alpha20 $alpha21 $alpha22 $mu3slow $mu3fast $n3slow $n3fast $alpha30 $alpha31 $alpha32 $W $uy $kvc $kvt $minFv $maxMuFac $tol |
| $eleTag | = unique element object tag |
| $iNode $jNode | = end nodes |
| $L1, $L2, $L3 | = effective radii. Li = R_i - h_i (see Figure 1) |
| $d1, $d2, $d3 | = displacement limits of pendulums (Figure 1). Displacement limit of the bearing is 2$d1+$d2+$d3+$L1.$d3/$L3-$L1.$d2/$L2 |
| $mu1slow, $mu2slow, $mu3slow | = friction coefficients μ_1, μ_2, μ_3 at slow velocity at vertical load $W. |
| $mu1fast, $mu2fast, $mu3fast | = friction coefficients μ_1, μ_2, μ_3 at fast velocity at vertical load $W. |
| $n1slow, $n1fast | = n_slow, n_fast for friction coefficient μ_1. Similar meaning for $n2slow, $n2fast, $n3slow, $n3fast. |
| $alpha10, $alpha11, $alpha12 | = α_0, α_1, α_2 determining rate parameters a for friction coefficient μ_1. Similar meaning for $alpha20, $alpha21, $alpha22, $alpha30, $alpha31, $alpha32. |
| $W | = vertical force where $mu1slow, $mu2slow, $mu3slow, $mu1fast, $mu2fast, $mu3fast are specified. This axial force is also used for the first trial of the first analyzing step. |
| $uy | = lateral displacement where sliding of the bearing starts. Recommended value = 0.25 to 1 mm. A smaller value may cause convergence problem. |
| $kvc, $kvt | = compression k_vc and tension stiffness k_vt of the bearing. |
| $minFv (>=0) | = minimum vertical compression force in the bearing used for computing the horizontal tangent stiffness matrix from the normalized tangent stiffness matrix of the element. $minFv is substituted for the actual compressive force when it is less than $minFv, and prevents the element from using a negative stiffness matrix in the horizontal direction when uplift occurs. The vertical nodal force returned to nodes is always computed from $kvc (or $kvt) and vertical deformation, and thus is not affected by $minFv. |
| $maxMuFac | = factor for determining the maximum friction coefficients. This value prevents the friction coefficient from exceeding an unrealistic maximum value when the vertical force becomes very small. The maximum friction coefficient is determined from μ_fast, for example μ_1 ≤ $maxMuFac.$mu1fast. |
| $tol | = relative tolerance for checking the convergence of the element. Recommended value = 1.e-10 to 1.e-3. |
SPECIAL CASES:
1. Constant friction coefficients:
- μ_1=const: $n1slow = $n1fast = 1.0; $mu1slow = $mu1fast = μ_1; all other constants defining μ_1 are arbitrary.
2. Friction coefficients vary with velocity but are independent of vertical force:
- μ_1 is independent of vertical force: $n1slow = $n1fast = 1.0; $alpha10 = a (rate parameter); $alpha11 = $alpha12 = 0.
3. Friction coefficients vary with vertical force but are independent of velocity:
- μ_1 is independent on velocity: $n1slow = $n1fast; $mu1slow = $mu1fast; all other constants defining μ_1 are arbitrary.
4. Vertical-horizontal uncoupled bearing:
- Restrain vertical displacement of the 2 nodes and set $minFv = static vertical reaction of the bearing.
NOTES:
The current element requires 6 degree of freedoms at each node and defines the local coordinate system to be the same as the global coordinate system, where the vertical axis must be 3.
Since the element accounts for the vertical-horizontal coupling behavior of TPBs, the time step size in analysis of vertically stiff structures should be small enough so that the high frequency components in responses can be captured.
Rayleigh damping is automatically included when using Rayleigh command.
The height of the bearing (for computing overturning moment from horizontal force) is computed from the vertical distance between the two end nodes.
EXAMPLE:
element TripleFrictionPendulum 1 1 2 0.36 1.25 1.25 0.1 0.2 0.2 0.012 0.018 0.8 0.7 25.0 0.0 0.0 0.052 0.075 0.8 0.7 25.0 0.0 0.0 0.12 0.16 0.8 0.7 25.0 0.0 0.0 1000.0 0.0005 1.E6 1.0 0.1 3.0 1.E-5;
REFERENCES:
1) Dao ND, Ryan KL, Sato E, Sasaki T. Predicting the displacement of triple pendulum™ bearings in a full-scale shaking experiment using a three-dimensional element. Earthquake Engineering and Structural Dynamics, 2013.
2) Dao ND. Seismic Response of a Full-scale 5-story Steel Frame Building Isolated by Triple Pendulum Bearings under 3D Excitations. Dissertation, University of Nevada – Reno, 2012.
3) Fenz DM, Constantinou MC. Spherical sliding isolation bearings with adaptive behavior: Theory. Earthquake Engineering and Structural Dynamics 2008; 37(2):163-183.
4) Morgan TA, Mahin SA. The use of innovative base isolation systems to achieve complex seismic performance objectives. PEER-2011/06 2011.
5) Bowden FP, Tabor D. The friction and lubrication of solids – part II. Oxford University Press, London, Great Britain, 1964.
6) Constantinou MC, Mokha A, Reinhorn A. Teflon bearings in base isolation. II: Modeling. Journal of Structural Engineering (ASCE) 1990; 116(2): 455-474
Code Developed by: Nhan D. Dao, University of Nevada - Reno. E-mail: nhan.unr@gmail.com
| APPLICATION EXAMPLES |
Download these 3 ground motion files and change the extension ".tcl" to ".ATH" for EXAMPLES 2 to 7: Media:TCU065-E.tcl, Media:TCU065-N.tcl, Media:TCU065-V.tcl
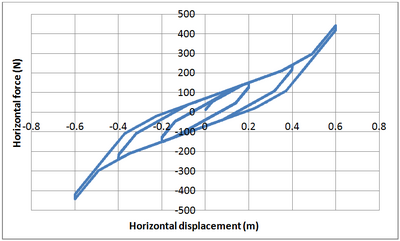
| EXAMPLE 1: |
Unidirectional static pushover of a TPB element with constant friction coefficients.
Tcl code: Media:CheckingTripleFrictionPendulum_StaticCyclicPushover1.tcl
Results:
| EXAMPLE 2: |
Unidirectional dynamic seismic analysis of a single mass supported by a TPB element with constant friction coefficients.
Tcl code: Media:CheckingTripleFrictionPendulum_1DDynamics_ConstFriction1.tcl
Results:
| EXAMPLE 3: |
Unidirectional dynamic seismic analysis of a single mass supported by a TPB element with variable friction coefficients.
Tcl code: Media:CheckingTripleFrictionPendulum_1DDynamics_VariableFriction1.tcl
Results:
| EXAMPLE 4: |
Two-dimensional dynamic seismic analysis of a single mass supported by a TPB element with constant friction coefficients.
Tcl code: Media:CheckingTripleFrictionPendulum_2DDynamic_ConstFriction1.tcl
Results:
| EXAMPLE 5: |
Two-dimensional dynamic seismic analysis of a single mass supported by a TPB element with variable friction coefficients.
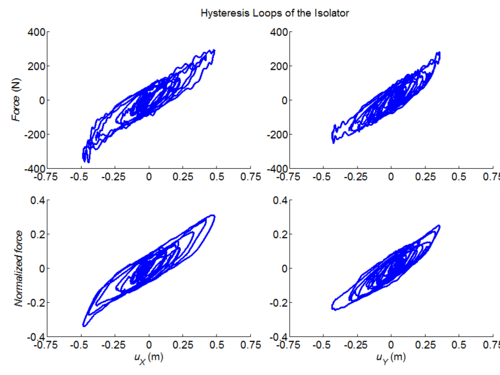
Tcl code: Media:CheckingTripleFrictionPendulum_2DDynamic_VariableFriction1.tcl
Results:
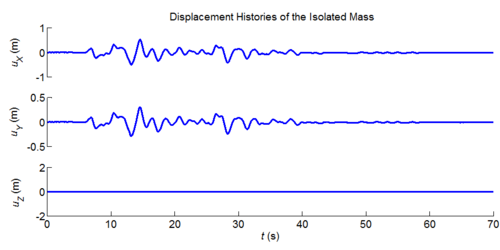
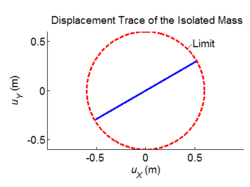
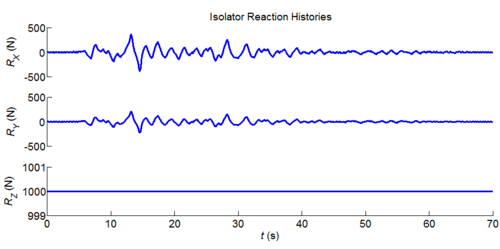
| EXAMPLE 6: |
Three-dimensional dynamic seismic analysis of a single mass supported by a TPB element with constant friction coefficients.
Tcl code: Media:CheckingTripleFrictionPendulum_3DDynamic_ConstFriction1.tcl
Results:
| EXAMPLE 7: |
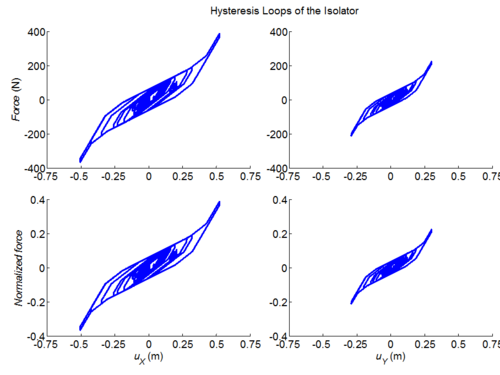
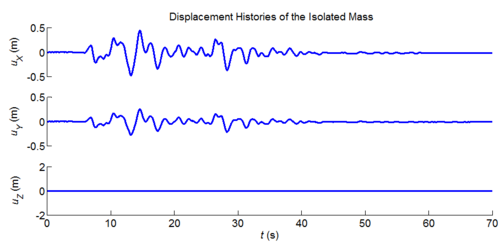
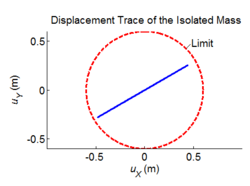
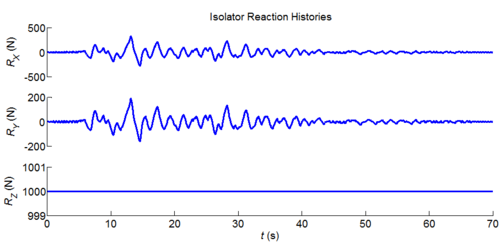
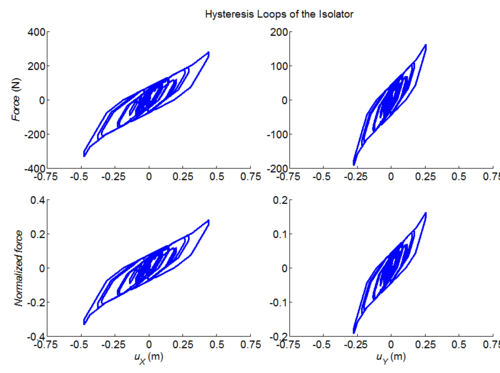
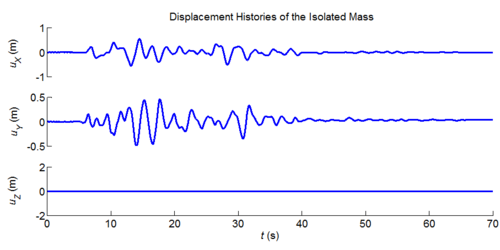
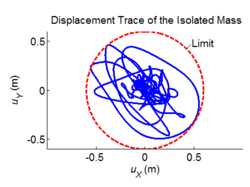
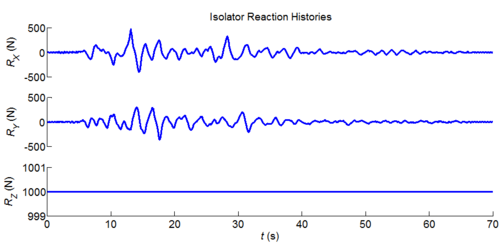
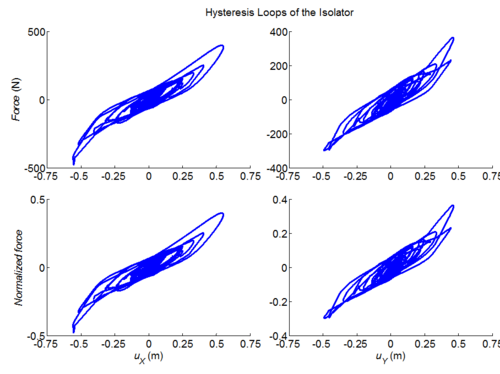
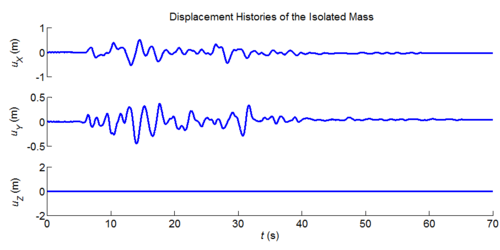
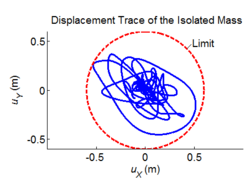
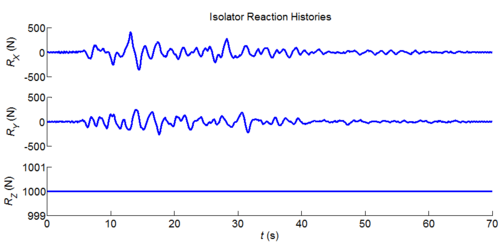
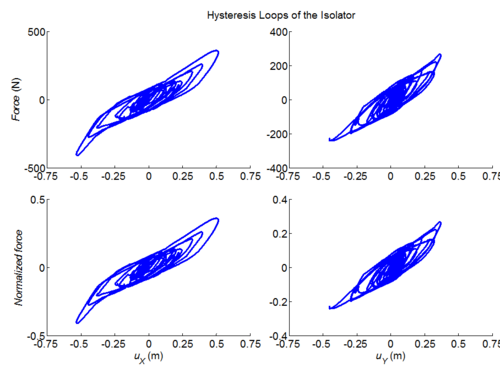
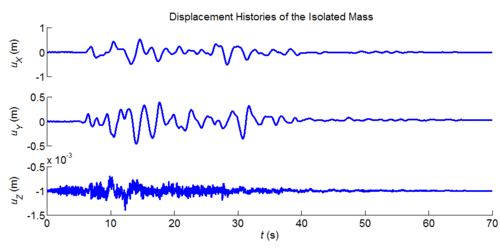
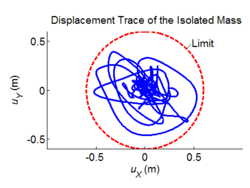
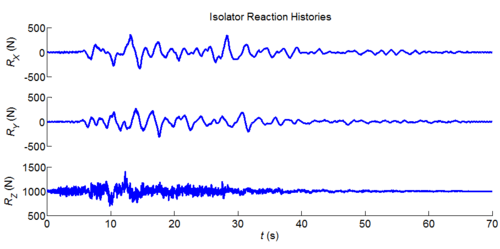
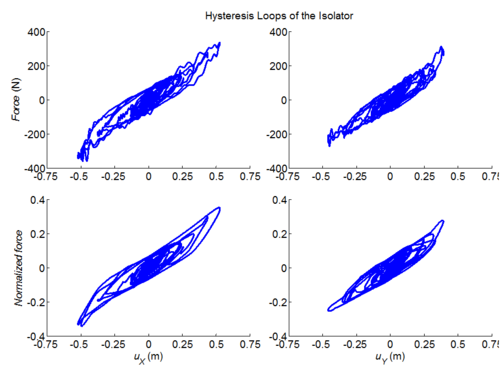
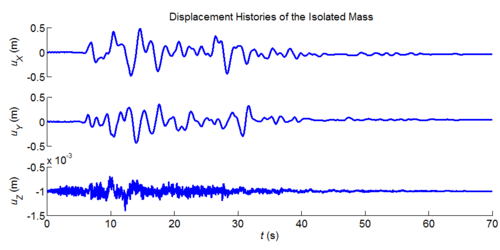
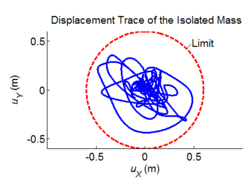
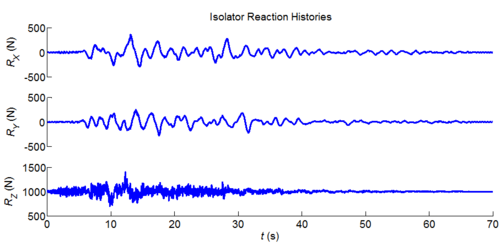
Three-dimensional dynamic seismic analysis of a single mass supported by a TPB element with variable friction coefficients.
Tcl code: Media:CheckingTripleFrictionPendulum_3DDynamic_VariableFriction1.tcl
Results: