Velocity Dependent Friction: Difference between revisions
No edit summary |
No edit summary |
||
| Line 22: | Line 22: | ||
<math>\[\mu = {\mu _{fast}} - \left( {{\mu _{fast}} - {\mu _{slow}}} \right) \cdot {e^{ - transRate\, \cdot \,\left| v \right|}}\]</math> | <math>{{formula}}\[\mu = {\mu _{fast}} - \left( {{\mu _{fast}} - {\mu _{slow}}} \right) \cdot {e^{ - transRate\, \cdot \,\left| v \right|}}\]{{formula}}</math> | ||
Revision as of 23:15, 23 January 2012
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
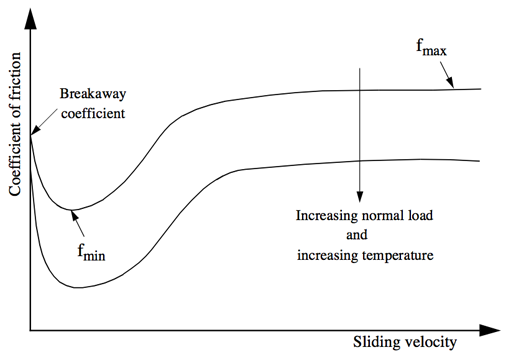
This command is used to construct a VDependent friction model object. It is useful for modeling the behavior of "PTFE" or PTFE-like materials sliding on a stainless steel surface. For a detailed presentation on the velocity dependence of such interfaces please refer to Constantinou et al. (1999).
| frictionModel VDependent $frnTag $muSlow $muFast $transRate |
| $frnTag | unique friction model object tag |
| $muSlow | coefficient of friction at low velocity |
| $muFast | coefficient of friction at high velocity |
| $transRate | transition rate from low to high velocity |
<math>\[\mu = {\mu _{fast}} - \left( {{\mu _{fast}} - {\mu _{slow}}} \right) \cdot {e^{ - transRate\, \cdot \,\left| v \right|}}\]\[\mu = {\mu _{fast}} - \left( {{\mu _{fast}} - {\mu _{slow}}} \right) \cdot {e^{ - transRate\, \cdot \,\left| v \right|}}\]\[\mu = {\mu _{fast}} - \left( {{\mu _{fast}} - {\mu _{slow}}} \right) \cdot {e^{ - transRate\, \cdot \,\left| v \right|}}\]</math>
EXAMPLE:
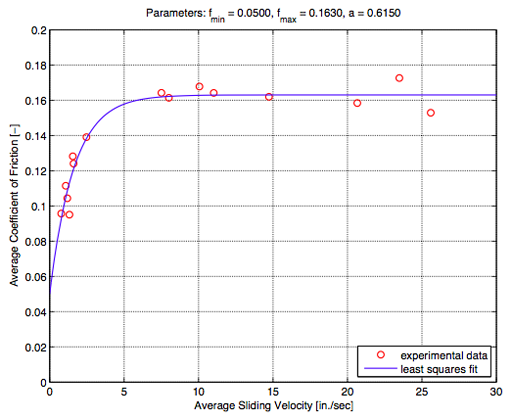
frictionModel VDependent 1 0.05 0.163 0.615
REFERENCE:
Constantinou, M.C., Tsopelas, P., Kasalanati, A., and Wolff, E.D. (1999). “Property modification factors for seismic isolation bearings”. Report MCEER-99-0012, Multidisciplinary Center for Earthquake Engineering Research, State University of New York.
Code Developed by: Andreas Schellenberg, University of California, Berkeley.