Maxwell Material: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 36: | Line 36: | ||
|- | |- | ||
| uniaxialMaterial Maxwell 1 150.0 100.0 0.30 5000.0 | | uniaxialMaterial Maxwell 1 150.0 100.0 0.30 5000.0 | ||
|- | |||
|- | |||
| Using these properties a comparison between simulated responses from OpenSees and a MATLAB based program are shown in Fig.1 | |||
|- | |||
[[File:Fig1.png]] to use the full version of the file | |||
|- | |- | ||
|- | |- | ||
Revision as of 18:08, 15 February 2011
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
This command is used to construct a Maxwell material (linear spring and nonlinear dashpot in series). The Maxwell material simulates the hysteretic response of viscous dampers.
| uniaxialMaterial Maxwell $matTag $K $C $a $L |
| $matTag | integer tag identifying material |
| $K | Elastic stiffness of linear spring (to model elastic stiffness of viscous damper) |
| $C | Viscous parameter of damper |
| $a | Viscous damper exponent |
| $L | Viscous damper length |
Examples:
 to use the full version of the file
to use the full version of the file
| 1. Input parameters: |
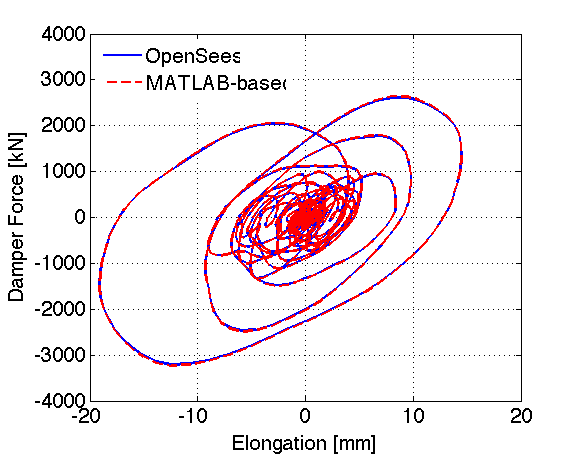
| Assume a viscous damper with axial stiffness K=150.0kN/mm, viscous parameter C = 100.0kN/(mm/s)^0.3, an exponent a=0.3 and length equal to 5000mm. |
| The input parameters for the material should be as follows: |
| uniaxialMaterial Maxwell 1 150.0 100.0 0.30 5000.0 |
| Using these properties a comparison between simulated responses from OpenSees and a MATLAB based program are shown in Fig.1 |
| 2. Tcl input file for Viscous Damper Calibration: |
| 3. OpenSees Example of 1-story steel moment frame with a viscous damper: |
References:
| [1] | Olsson, A.K., and Austrell, P-E., (2001), "A fitting procedure for viscoelastic-elastoplastic material models," Proceedings of the Second European Conference on Constitutive Models for Rubber, Germany, 2001. |
| [2] | Ottosen, N.S., and Ristinmaa, M., (1999). "The mechanics of constitutive modelling, (Numerical and thermodynamical topics)," Lund University,Division of Solid Mechanics, Sweden, 1999. |
Code Developed by : by Dr. Dimitrios G. Lignos (McGill University)