FRPConfinedConcrete

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

This command is used to construct a uniaxial Megalooikonomou-Monti-Santini concrete material object with degraded linear unloading/reloading stiffness according to the work of Karsan-Jirsa and no tensile strength.

uniaxialMaterial FRPConfinedConcrete $matTag $fpc1 $fpc2 $epsc0 $D $c $Ej $Sj $tj $eju $S $fyl $fyh $dlong $dtrans $Es $vo $k $useBuck

---

$matTag	integer tag identifying material.
$fpc1	concrete core compressive strength.
$fpc2	concrete cover compressive strength.
$epsc0	strain corresponding to unconfined concrete strength.
$D	diameter of the circular section.
$c	dimension of concrete cover (until the outer edge of steel stirrups)
$Ej	elastic modulus of the fiber reinforced polymer (FRP) jacket.
$Sj	clear spacing of the FRP strips - zero if FRP jacket is continuous.
$tj	total thickness of the FRP jacket.
$eju	rupture strain of the FRP jacket from tensile coupons.
$S	spacing of the steel spiral/stirrups.
$fyl	yielding strength of longitudinal steel bars.
$fyh	yielding strength of the steel spiral/stirrups.
$dlong	diameter of the longitudinal bars of the circular section.
$dtrans	diameter of the steel spiral/stirrups.
$Es	elastic modulus of steel.
$vo	initial Poisson’s coefficient for concrete.
$k	reduction factor for the rupture strain of the FRP jacket, recommended values 0.5-0.8.
$useBuck	FRP jacket failure criterion due to buckling of longitudinal compressive steel bars (0 = not include it, 1= to include it).

NOTES:

• IMPORTANT: The units of the input parameters should be in MPa, N, mm.

• Concrete compressive strengths and the corresponding strain should be input as positive values.

• When rupture of FRP jacket occurs due to dilation of concrete (lateral concrete strain exceeding reduced rupture strain of FRP jacket), the analysis is not terminated. Only a message “FRP Rupture” is plotted on the screen.

• When rupture of FRP jacket occurs due to its interaction with buckled longitudinal compressive steel bars, the analysis is not terminated. Only a message “"FRP Rupture due to Buckling of Long.Bar under compression"” is plotted on the screen.

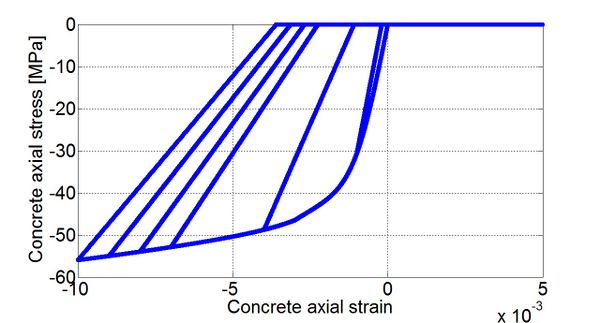
Typical Hysteretic Stress-Strain Relation for FRPConfinedConcrete.

EXAMPLES:

Example: Cantilever FRP-Confined Circular Reinforced Concrete Column under Cyclic Lateral Loading

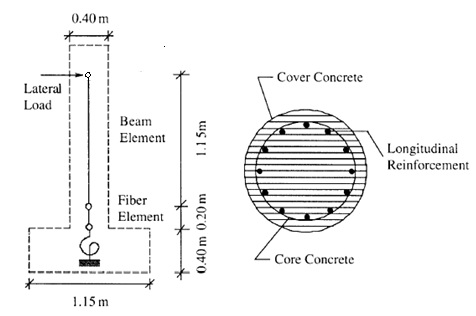
Cantilever Column Model Definition.

The cantilever column was modeled by a linear beam element with the stiffness corresponding to flexural yielding and a fiber element used to capture the flexural hysteretic behavior at the plastic hinge. The length of the fiber element was assumed to be half of the column’s diameter. A rotational spring at the bottom of the column represents the longitudinal bar pullout from the footing and was assumed to have an elastic stiffness. According to FRPConfinedConcrete model, the averaged response of the two different regions - concrete core (confined by both the FRP & the existing reinforcement) and concrete cover (confined only with the FRP wrap) - in the cross-section allows the assignment of a unique stress-strain law (FRPConfinedConcrete) to all the concrete fibers/layers of the circular section.

File:ExampleFRP.tcl

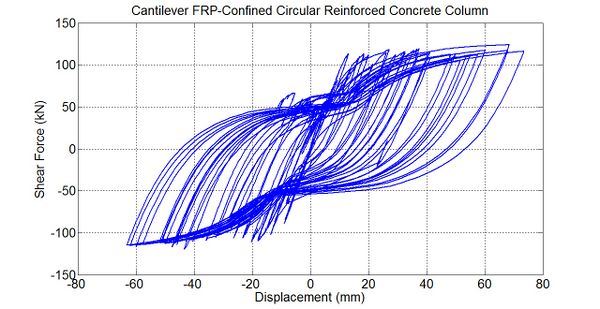
Response of Cantilever FRP-Confined Circular Reinforced Concrete Column under Cyclic Lateral Loading.

---

REFERENCES:

• MEGALOOIKONOMOU K.G., MONTI G., SANTINI S., “Constitutive Model for Fiber –Reinforced Polymer - and Tie – Confined Concrete”, ACI Structural Journal, Vol. 109, No. 4, July 2012, pp. 569-578.

• KARSAN, I.D., JIRSA, J.O., “Behaviour of concrete under compressive loadings”, Journal of Structural Division ASCE, Vol. 95, No. 12, 1969, pp. 2543-2563.

• PAPAVASILEIOU G.S., MEGALOOIKONOMOU K.G., “Numerical Simulation of FRP-Confined Circular Bridge Piers Using OpenSees”, In Proceedings of: OpenSees Days Italy (OSD), Second International Conference, University of Salerno, Fisciano, Salerno, Italy, June 10-11, 2015.

• MEGALOOIKONOMOU K.G., MONTI G., "Numerical Modeling of FRP-Retrofitted Circular RC Columns Including Shear", In Proceedings of: 5th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (COMPDYN 2015), Crete Island, Greece, May 25 - 27, 2015.

• GALLARDO – ZAFRA R., KAWASHIMA, K., “Analysis of CFRP RC Bridge Columns under Lateral Cyclic Loading”, Journal of Earthquake Engineering, Vol. 13, 2009, pp. 129-154.

---

Code Developed By:

Konstantinos G. Megalooikonomou, Onassis Foundation Scholar, University of Cyprus (Webpage: www.bigeconomy.gr/en/).