KikuchiAikenLRB Material: Difference between revisions
No edit summary |
No edit summary |
||
| Line 41: | Line 41: | ||
{| | {| | ||
|- | |- | ||
| '''1''' || lead-rubber bearing | | '''1''' || lead-rubber bearing, up to 400% shear strain [Kikuchi et al., 2010 & 2012] | ||
|} | |} | ||
| Line 64: | Line 64: | ||
REFERENCES: | REFERENCES: | ||
M. Kikuchi , I. D. Aiken and A. Kasalanati , "Simulation analysis for the ultimate behavior of full-scale lead-rubber seismic isolation bearings", ''15th World Conference on Earthquake Engineering'', No. 1688, 2012. | M. Kikuchi, T. Nakamura, I. D. Aiken, "Three-dimensional analysis for square seismic isolation bearings under large shear deformations and high axial loads", ''Earthquake Engineering and Structural Dynamics'', Vol. 39, 1513-1531, 2010. | ||
M. Kikuchi , I. D. Aiken, A. Kasalanati , "Simulation analysis for the ultimate behavior of full-scale lead-rubber seismic isolation bearings", ''15th World Conference on Earthquake Engineering'', No. 1688, 2012. | |||
---- | ---- | ||
Code Developed by: <span style="color:blue"> mkiku </span> | Code Developed by: <span style="color:blue"> mkiku </span> | ||
Latest revision as of 17:46, 13 March 2018
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
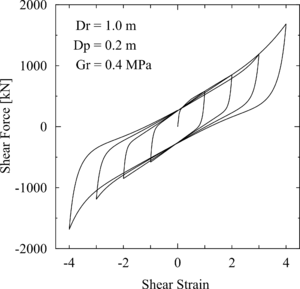
This command is used to construct a uniaxial KikuchiAikenLRB material object. This material model produces nonlinear hysteretic curves of lead-rubber bearings.
| uniaxialMaterial KikuchiAikenLRB $matTag $type $ar $hr $gr $ap $tp $alph $beta <-T $temp> <-coKQ $rk $rq> <-coMSS $rs $rf> |
| $matTag | integer tag identifying material |
| $type | rubber type (see note 1) |
| $ar | area of rubber [unit: m^2] |
| $hr | total thickness of rubber [unit: m] |
| $gr | shear modulus of rubber [unit: N/m^2] |
| $ap | area of lead plug [unit: m^2] |
| $tp | yield stress of lead plug [unit: N/m^2] |
| $alph | shear modulus of lead plug [unit: N/m^2] |
| $beta | ratio of initial stiffness to yielding stiffness |
| $temp | temperature [unit: °C] |
| $rk $rq | reduction rate for yielding stiffness ($rk) and force at zero displacement ($rq) |
| $rs $rf | reduction rate for stiffness ($rs) and force ($rf) (see note 3) |
NOTES:
1) Following rubber types for $type are available:
| 1 | lead-rubber bearing, up to 400% shear strain [Kikuchi et al., 2010 & 2012] |
2) This material uses SI unit in calculation formula. Input arguments must be converted into [m], [m^2], [N/m^2].
3) $rs and $rf are available if this material is applied to multipleShearSpring (MSS) element. Recommended values are $rs=1/sum(i=0,n-1){ sin(pi*i/n)^2} and $rf=1/sum(i=0,n-1){sin(pi*i/n)}, where n is the number of springs in the MSS. For example, when n=8, $rs=0.2500 and $rf=0.1989.
EXAMPLE:
REFERENCES:
M. Kikuchi, T. Nakamura, I. D. Aiken, "Three-dimensional analysis for square seismic isolation bearings under large shear deformations and high axial loads", Earthquake Engineering and Structural Dynamics, Vol. 39, 1513-1531, 2010.
M. Kikuchi , I. D. Aiken, A. Kasalanati , "Simulation analysis for the ultimate behavior of full-scale lead-rubber seismic isolation bearings", 15th World Conference on Earthquake Engineering, No. 1688, 2012.
Code Developed by: mkiku