BilinearOilDamper Material: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 51: | Line 51: | ||
|- | |- | ||
|- | |- | ||
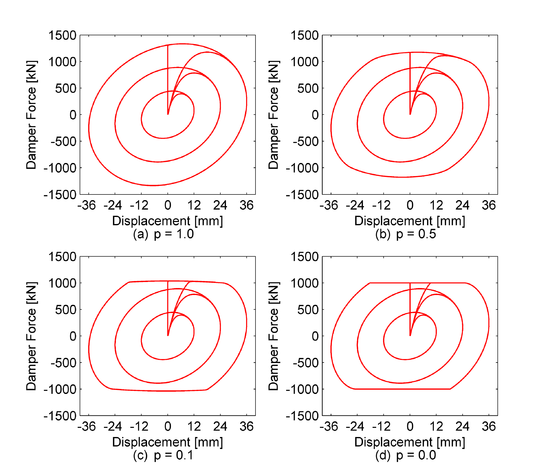
| [[File:BOD_1.png|550px|thumb|left| Oil Damper with various | | [[File:BOD_1.png|550px|thumb|left| Oil Damper with various post-relief viscous damping coefficient ratios]] | ||
|- | |- | ||
|- | |- | ||
| Line 65: | Line 65: | ||
|- | |- | ||
|- | |- | ||
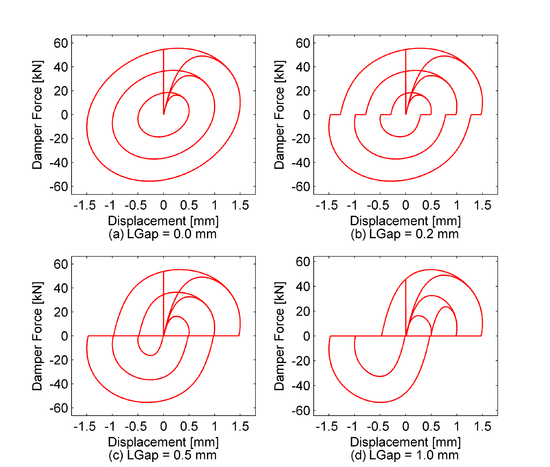
| [[File:BODgap_2.png|550px|thumb|left| Oil Damper with various | | [[File:BODgap_2.png|550px|thumb|left| Oil Damper with various gap lengths]] | ||
|- | |- | ||
|- | |- | ||
Revision as of 16:12, 15 June 2017
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
This command is used to construct a BilinearOilDamper material, which simulates the hysteretic response of bilinear oil dampers with relief valve. Two adaptive iterative algorithms have been implemented and validated to solve numerically the constitutive equations within a bilinear oil damper with a high-precision accuracy.
| uniaxialMaterial BilinearOilDamper $matTag $K $Cd <$Fr $p> <$LGap> < $NM $RelTol $AbsTol $MaxHalf> |
| $matTag | integer tag identifying material |
| $K | Elastic stiffness of linear spring to model the axial flexibility of an oil damper (brace and damper portion) |
| $Cd | Viscous damping coefficient of an oil damper (before relief) |
| $Fr | Damper relief load (default=1.0, Damper property) |
| $p | Post-relief viscous damping coefficient ratio (default=1.0, linear oil damper) |
| $LGap | gap length to simulate the gap length due to the pin tolerance (default=0.0: zero tolerance) |
| $NM | Employed adaptive numerical algorithm (default value NM = 1; 1 = Dormand-Prince54, 2=adaptive finite difference) |
| $RelTol | Tolerance for absolute relative error control of the adaptive iterative algorithm (default value 10^-6) |
| $AbsTol | Tolerance for absolute error control of adaptive iterative algorithm (default value 10^-10) |
| $MaxHalf | Maximum number of sub-step iterations within an integration step (default value 15) |
Examples:
| 1. Input parameters: |
| Assume a bilinear oil damper with axial stiffness K=200.0kN/mm, viscous damping coefficient C=6.0KN/(mm/s), relief load Fr=1000.0KN, p=0.1. |
| The input parameters for the material should be as follows: |
| uniaxialMaterial BilinearOilDamper 1 200.0 6.0 1000 0.1 |
| Using these properties, Figure 1c shows the hysteretic response of this damper for sinusoidal displacement increments of 12, 24 and 36mm and a frequency f = 1.0Hz. Figures 1a-1d show the damper hysteresis with varying post-relief viscous damping coefficient ratio (p=1.0, 0.5, 0.1, 0.0). |
 |
| Assume a bilinear oil damper with axial stiffness K=200.0kN/mm, viscous damping coefficient C=6.0KN/(mm/s), relief load Fr=1000.0KN, p=0.1 and LGap = 0.5mm due to the pin tolerance at the damper ends. |
| The input parameters for the material should be as follows: |
| uniaxialMaterial BilinearOilDamper 1 200.0 6.0 1000 0.1 0.5 |
| Using these properties, Figure 2c shows the hysteretic response of this damper for sinusoidal displacement increments of 0.5, 1 and 1.5mm and a frequency f = 1.0Hz. Figures 2a-2d show the damper hysteresis with varying gap length (LGap = 0.0, 0.2. 0.5. 1.0 mm) |
 |
References:
| [1] | Akcelyan, S. (2017). "Seismic retrofit of existing steel tall buildings with supplemental damping devices." Ph.D. Dissertation, McGill University, Canada. |
Code Developed and Implemented by : Sarven Akcelyan & Prof. Dimitrios G. Lignos, (McGill University)