Modified Ibarra-Medina-Krawinkler Deterioration Model with Peak-Oriented Hysteretic Response (ModIMKPeakOriented Material)

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

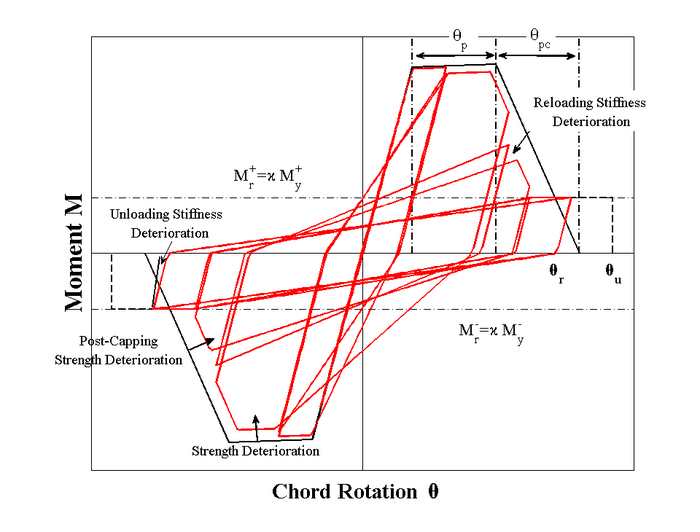
This command is used to construct a ModIMKPeakOriented material. This material simulates the modified Ibarra-Medina-Krawinkler deterioration model with peak-oriented hysteretic response. Note that the hysteretic response of this material has been calibrated with respect to 200 experimental data of RC beams in order to estimate the deterioration parameters of the model. This information was developed by Lignos and Krawinkler (2012). NOTE: before you use this material make sure that you have downloaded the latest OpenSees version.. A youtube video presents a summary of this model including the way to be used within openSees (http://youtu.be/YHBHQ-xuybE).

uniaxialMaterial ModIMKPeakOriented $matTag $K0 $as_Plus $as_Neg $My_Plus $My_Neg $Lamda_S $Lamda_C $Lamda_A $Lamda_K $c_S $c_C $c_A $c_K $theta_p_Plus $theta_p_Neg $theta_pc_Plus $theta_pc_Neg $Res_Pos $Res_Neg $theta_u_Plus $theta_u_Neg $D_Plus $D_Neg

---

$matTag	integer tag identifying material
$K0	elastic stiffness
$as_Plus	strain hardening ratio for positive loading direction
$as_Neg	strain hardening ratio for negative loading direction
$My_Plus	effective yield strength for positive loading direction
$My_Neg	effective yield strength for negative loading direction (negative value)
$Lamda_S	Cyclic deterioration parameter for strength deterioration [E_t=Lambda*M_y, see Lignos and Krawinkler (2011); set Lambda = 0 to disable this mode of deterioration]
$Lamda_C	Cyclic deterioration parameter for post-capping strength deterioration [E_t=Lambda*M_y, see Lignos and Krawinkler (2011); set Lambda = 0 to disable this mode of deterioration]
$Lamda_A	Cyclic deterioration parameter for acceleration reloading stiffness deterioration [E_t=Lambda*M_y, see Lignos and Krawinkler (2011); set Lambda = 0 to disable this mode of deterioration]
$Lamda_K	Cyclic deterioration parameter for unloading stiffness deterioration [E_t=Lambda*M_y, see Lignos and Krawinkler (2011); set Lambda = 0 to disable this mode of deterioration]
$c_S	rate of strength deterioration. The default value is 1.0.
$c_C	rate of post-capping strength deterioration. The default value is 1.0.
$c_A	rate of accelerated reloading deterioration. The default value is 1.0.
$c_K	rate of unloading stiffness deterioration. The default value is 1.0.
$theta_p_Plus	pre-capping rotation for positive loading direction (often noted as plastic rotation capacity)
$theta_p_Neg	pre-capping rotation for negative loading direction (often noted as plastic rotation capacity) (must be defined as a positive value)
$theta_pc_Plus	post-capping rotation for positive loading direction
$theta_pc_Neg	post-capping rotation for negative loading direction (must be defined as a positive value)
$Res_Pos	residual strength ratio for positive loading direction
$Res_Neg	residual strength ratio for negative loading direction (must be defined as a positive value)
$theta_u_Plus	ultimate rotation capacity for positive loading direction
$theta_u_Neg	ultimate rotation capacity for negative loading direction (must be defined as a positive value)
$D_Plus	rate of cyclic deterioration in the positive loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0.
$D_Neg	rate of cyclic deterioration in the negative loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0.

Image from: Lignos and Krawinkler (2012)

The deterioration model parameters can be calibrated based on actual experimental data of RC beams in terms of load - displacement or moment - rotation. Examples of such calibrations can be found in Lignos (2008) and Lignos and Krawinkler (2012).

---

References:

[1]	Lignos, D.G., Krawinkler, H. (2012). “Development and Utilization of Structural Component Databases for Performance-Based Earthquake Engineering", Journal of Structural Engineering, ASCE, doi: 10.1061/(ASCE)ST.1943-541X.0000646.
[2]	Lignos, D.G., and Krawinkler, H. (2011). “Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading”, Journal of Structural Engineering, ASCE, Vol. 137 (11), 1291-1302.
[3]	Lignos, D.G. and Krawinkler, H. (2012). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Rep.No.TB 177, The John A. Blume Earthquake Engineering Research Center, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports]
[4]	Lignos, D.G. (2008). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Ph.D. Dissertation, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA.
[5]	Ibarra L.F., and Krawinkler, H. (2005). “Global collapse of frame structures under seismic excitations”, Rep. No. TB 152, The John A. Blume Earthquake Engineering Center, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports]
[6]	Ibarra L.F., Medina R. A., and Krawinkler H. (2005). “Hysteretic models that incorporate strength and stiffness deterioration”, Earthquake Engineering and Structural Dynamics, 34(12), 1489-1511.

Code Developed by : by Dr. Dimitrios G. Lignos, McGill University