FRPConfinedConcrete: Difference between revisions
No edit summary |
No edit summary |
||
| Line 68: | Line 68: | ||
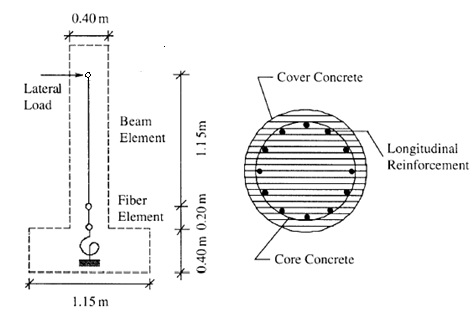
'''Cantilever Column Model Definition.''' | '''Cantilever Column Model Definition.''' | ||
[[File: | [[File:Figure_2.jpg|600px]] | ||
The cantilever column was modeled by a linear beam element with the stiffness corresponding to flexural yielding and a fiber element used to capture the flexural hysteretic behavior at the plastic hinge. The length of the fiber element was assumed to be half of the column’s diameter. A rotational spring at the bottom of the column represents the longitudinal bar pullout from the footing and was assumed to have an elastic stiffness. | The cantilever column was modeled by a linear beam element with the stiffness corresponding to flexural yielding and a fiber element used to capture the flexural hysteretic behavior at the plastic hinge. The length of the fiber element was assumed to be half of the column’s diameter. A rotational spring at the bottom of the column represents the longitudinal bar pullout from the footing and was assumed to have an elastic stiffness. | ||
[[File:ExampleFRP.tcl]] | |||
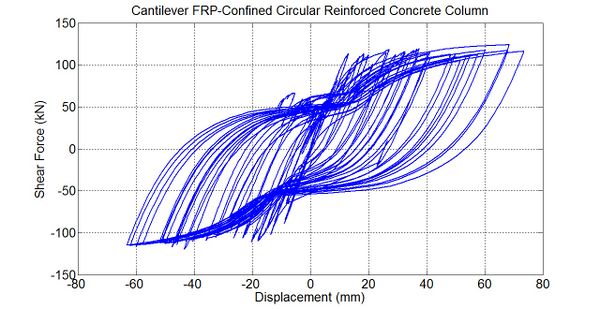
'''Response of Cantilever FRP-Confined Circular Reinforced Concrete Column under Cyclic Lateral Loading.''' | '''Response of Cantilever FRP-Confined Circular Reinforced Concrete Column under Cyclic Lateral Loading.''' | ||
[[File: | [[File:Figure_3.jpg|600px]] | ||
Revision as of 20:18, 7 June 2015
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
This command is used to construct a uniaxial Megalooikonomou-Monti-Santini concrete material object with degraded linear unloading/reloading stiffness according to the work of Karsan-Jirsa and no tensile strength.
| uniaxialMaterial FRPConfinedConcrete $matTag $fpc1 $fpc2 $epsc0 $D $c $Ej $Sj $tj $eju $S $fyh $dlong $dtrans $Es $vo $k |
| $matTag | integer tag identifying material. |
| $fpc1 | concrete core compressive strength. |
| $fpc2 | concrete cover compressive strength. |
| $epsc0 | strain corresponding to unconfined concrete strength. |
| $D | diameter of the circular section. |
| $c | dimension of concrete cover (until the edge of steel stirrups) |
| $Ej | elastic modulus of the fiber reinforced polymer (FRP) jacket. |
| $Sj | clear spacing of the FRP strips - zero if it's continuous. |
| $tj | total thickness of the FRP jacket. |
| $eju | rupture strain of the FRP jacket from tensile coupons. |
| $S | spacing of the steel spiral/stirrups. |
| $fyh | yielding strength of the steel spiral/stirrups. |
| $dlong | diameter of the longitudinal bars of the circular section. |
| $dtrans | diameter of the steel spiral/stirrups. |
| $Es | elastic modulus of steel. |
| $vo | initial Poisson’s coefficient for concrete. |
| $k | reduction factor for the rupture strain of the FRP jacket, recommended values 0.5-0.8.. |
NOTES:
• IMPORTANT: The units of the input parameters should be in MPa, N, mm.
• Concrete compressive strengths and the corresponding strain should be input as positive values.
• When rupture of FRP jacket occurs due to dilation of concrete (lateral concrete strain exceeding reduced rupture strain of FRP jacket), the analysis is not terminated. Only a message “FRP Rupture” is plotted on the screen.
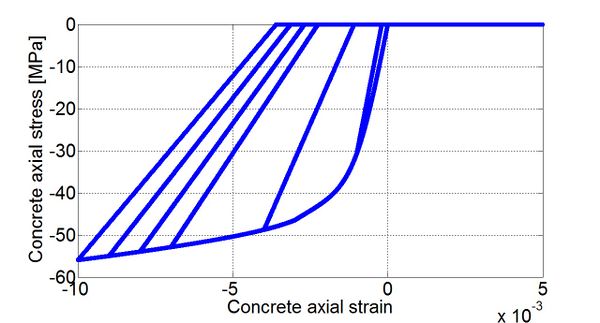
Typical Hysteretic Stress-Strain Relation for FRPConfinedConcrete.
EXAMPLES:
Example: Cantilever FRP-Confined Circular Reinforced Concrete Column under Cyclic Lateral Loading
Cantilever Column Model Definition.
The cantilever column was modeled by a linear beam element with the stiffness corresponding to flexural yielding and a fiber element used to capture the flexural hysteretic behavior at the plastic hinge. The length of the fiber element was assumed to be half of the column’s diameter. A rotational spring at the bottom of the column represents the longitudinal bar pullout from the footing and was assumed to have an elastic stiffness.
Response of Cantilever FRP-Confined Circular Reinforced Concrete Column under Cyclic Lateral Loading.
REFEERENCES:
• MEGALOOIKONOMOU K.G., MONTI G., SANTINI S., “Constitutive Model for Fiber –Reinforced Polymer - and Tie – Confined Concrete”, ACI Structural Journal, Vol. 109, No. 4, July 2012, pp. 569-578.
• KARSAN, I.D., JIRSA, J.O., “Behaviour of concrete under compressive loadings”, Journal of Structural Division ASCE, Vol. 95, No. 12, 1969, pp. 2543-2563.
• PAPAVASILEIOU G.S., MEGALOOIKONOMOU K.G., “Numerical Simulation of FRP-Confined Circular Bridge Piers Using Opensees”, In Proceedings of: Opensees Days Italy (OSD), Second Italian Conference, University of Salerno, Fisciano, Salerno, Italy, June 10-11, 2015.
• GALLARDO – ZAFRA R., KAWASHIMA, K., “Analysis of CFRP RC Bridge Columns under Lateral Cyclic Loading”, Journal of Earthquake Engineering, Vol. 13, 2009, pp. 129-154.