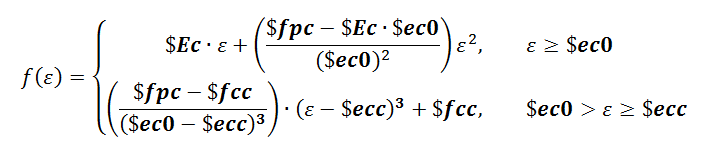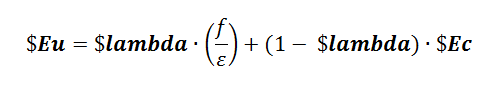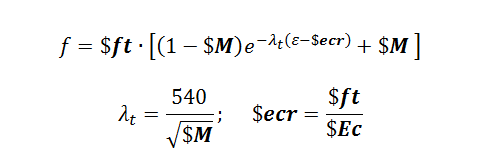ConcretewBeta Material: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 57: | Line 57: | ||
==Implementation== | ==Implementation== | ||
::[[File:ConcwBeta_Eq1a.png|thumb|upright=2.5|Equation 1.]] | |||
::[[File:ConcwBeta_Eq2a.png|thumb|upright=1.8|Equation 2.]] | |||
::[[File:ConcwBeta_Eq3.png|thumb|upright=1.8|Equation 3.]] | |||
===Uniaxial Behavior=== | ===Uniaxial Behavior=== | ||
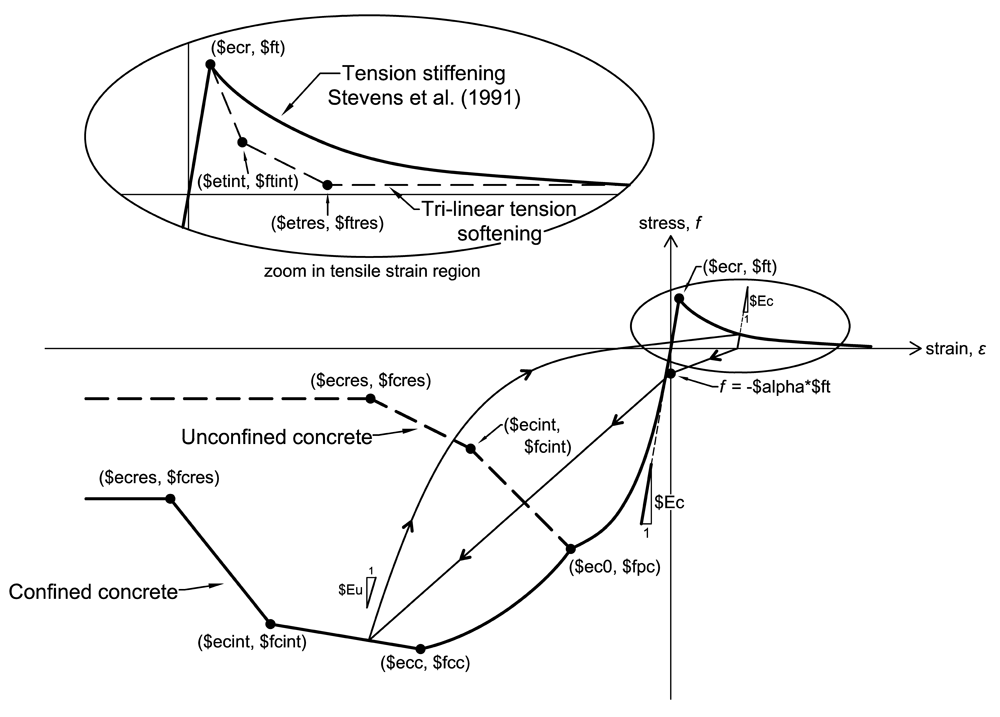
  Figure 1 shows the compression and tension envelopes and the input parameters. The confined concrete envelope is defined by Equation 1 up to strain '''$ecc'''. The default values of '''$fcc''' and '''$$ecc''' are equal to '''$fpc''' and '''$ec0''', respectively, for an an unconfined behavior. Following this region, the compression envelope is tri-linear and passes through the points ('''$ecint''', '''$fcint''') and ('''$ecres''', '''$fcres''') in that order. For compression strains larger than '''$ecres''', the residual stress is '''$fcres'''. | |||
  For compression strain, the slope of the unloading branch is defined by Equation 2. After reaching zero stress, the material reloads linearly to the point with the largest tensile strain that occurred before. | |||
  For compression strain, the slope of the unloading branch is | |||
After reaching zero stress, the material reloads linearly to the point with the largest tensile strain that occurred before. | |||
  The tension envelope is linear until it reaches '''$ft'''. If the tension stiffening parameter '''$M''' is not specified, the tension envelope after reaching '''$ft''' is tri-linear and passes through the points ('''$etint''', '''$ftint''') and ('''$etres''', '''$ftres''') in that order. For tensile strains larger than '''$etres''', the residual stress is '''$fcres'''. |   The tension envelope is linear until it reaches '''$ft'''. If the tension stiffening parameter '''$M''' is not specified, the tension envelope after reaching '''$ft''' is tri-linear and passes through the points ('''$etint''', '''$ftint''') and ('''$etres''', '''$ftres''') in that order. For tensile strains larger than '''$etres''', the residual stress is '''$fcres'''. | ||
  If '''$M''' is specified, the nonlinear tension stiffening behavior |   If '''$M''' is specified, the nonlinear tension stiffening behavior defined by Equation 3. It is suggested that '''$M''' = (75 mm)*''ρ<sub>l</sub>''/''d<sub>b</sub>'' where ''ρ<sub>l</sub>'' is the steel ratio in the direction parallel to the material direction and ''d<sub>b</sub>'' is the bar diameter in mm. | ||
It is suggested that '''$M''' = (75 mm)*''ρ<sub>l</sub>''/''d<sub>b</sub>'' where ''ρ<sub>l</sub>'' is the steel ratio in the direction parallel to the material direction and ''d<sub>b</sub>'' is the bar diameter in mm. | |||
  The material unloads from tension strain using a slope of '''$Ec'''. After reaching zero stress, the material targets the point (0, -'''$alpha'''*'''$ft'''). Thereafter, the material loads linearly to the point where the peak compressive strain previously occurred. In the case where the slope leading to this target point is less than that for the point (0, -'''$alpha'''*'''$ft'''), the material reloads directly to the point where peak compressive strain occurred. |   The material unloads from tension strain using a slope of '''$Ec'''. After reaching zero stress, the material targets the point (0, -'''$alpha'''*'''$ft'''). Thereafter, the material loads linearly to the point where the peak compressive strain previously occurred. In the case where the slope leading to this target point is less than that for the point (0, -'''$alpha'''*'''$ft'''), the material reloads directly to the point where peak compressive strain occurred. | ||
::[[File:ConcwBeta_Fig1b.gif|thumb|center|upright=4.0|alt=ConcretewBeta Figure 1 |Figure 1. ConcretewBeta material model behavior based on specified input parameters]] | |||
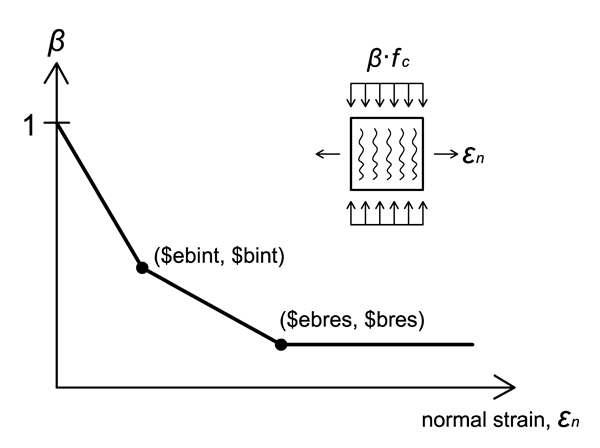
::[[File:ConcwBeta_Fig2b.gif|thumb|upright=2.0|alt=ConcretewBeta Figure 2 |Figure 2. Relation between the concrete compressive stress reduction factor, β, and normal tensile strain, ε<sub>n</sub> ]] | |||
===Biaxial Behavior=== | ===Biaxial Behavior=== | ||
  The ConcretewBeta material model accounts for the biaxial strain field on the concrete compressive behavior when used in conjunction with the '''[[Truss2 Element| Truss2]]''' element. The '''[[Truss2 Element| Truss2]]''' element computes the strain normal to the direction of the element (see '''[[Truss2 Element| Truss2 Element]]'''). |   The ConcretewBeta material model accounts for the biaxial strain field on the concrete compressive behavior when used in conjunction with the '''[[Truss2 Element| Truss2]]''' element. The '''[[Truss2 Element| Truss2]]''' element computes the strain normal to the direction of the element (see '''[[Truss2 Element| Truss2 Element]]'''). | ||
Revision as of 01:38, 7 September 2013
This command is used to construct a uniaxial concrete material object that explicitly considers for the effect of normal (to the axis where the material object is used) strain to the behavior of the concrete in compression. The compressive stress-strain envelope, up to the peak compressive strength(unconfined or confined) is based on the Fujii concrete model (Hoshikuma et al. 1997). The material has two options regarding the strength degradation in tension: (a) tri-linear or (b) nonlinear [based on the tension stiffening relation of Stevens et al (1991)]. The softening behavior in compression is tri-linear.
The model accounts for the effect of normal tensile strains on the concrete compressive behavior when used with the Truss2 or CorotTruss2 elements. See the Truss2 Element for description of how the normal strain is computed. The instantaneous stress is β*f where f is the computed stress and β is the compressive stress reduction factor which depends on the normal tensile strain, εn. The relation between εn and β (see the Biaxial Behavior Section) is tri-linear. Default values result in β = 1.
| uniaxialMaterial ConcretewBeta $matTag $fpc $ec0 $fcint $ecint $fcres $ecres $ft $ftint $etint $ftres $etres <-lambda $lambda> <-alpha $alpha> <-beta $bint $ebint $bres $ebres> <-M $M> <-E $Ec> <-conf $fcc $ecc> |
| $matTag | integer tag identifying material |
| $fpc | peak unconfined concrete compressive strength* |
| $ec0 | compressive strain corresponding to unconfined concrete compressive strength* |
| $fcint, $ecint | intermediate stress-strain point for compression post-peak envelope* |
| $fcres, $ecres | residual stress-strain point for compression post-peak envelope* |
| $ftint | tensile strength of concrete |
| $ftint, $etint | intermediate stress-strain point for tension softening envelope |
| $ftres, $etres | residual stress-strain point for tension softening envelope |
| Optional: | |
| $lambda | controls the path of unloading from compression strain (default 0.5) |
| $alpha | controls the path of unloading from tensile strain (default 1) |
| $bint $ebint | intermediate β-strain point for for biaxial effect (default 1 and 0, respectively) |
| $bres $ebres | residual β-strain point for for biaxial effect (default 1 and 0, respectively) |
| $M | factor for Stevens et al. (1991) tension stiffening (default 0; see Note 2) |
| $Ec | initial stiffness (default 2*$fpc/$ec0; see Note 3) |
| $fcc $ecc | confined concrete peak compressive stress and corresponding strain* (see Eq. 1) |
NOTES:
(1) *Parameters of concrete in compression should be specified as negative values.
(2) For non-zero $M, the tension stiffening behavior will govern the post-peak tension envelope. Tri-linear tension softening parameters $ftint, $etint, $ftres, $etres will have no effect, but dummy values must be specified.
(3) Value of $Ec must be between $fpc/$ec0 and 2*$fpc/$ec0 otherwise the closest value will be assigned.
Implementation
Uniaxial Behavior
Figure 1 shows the compression and tension envelopes and the input parameters. The confined concrete envelope is defined by Equation 1 up to strain $ecc. The default values of $fcc and $$ecc are equal to $fpc and $ec0, respectively, for an an unconfined behavior. Following this region, the compression envelope is tri-linear and passes through the points ($ecint, $fcint) and ($ecres, $fcres) in that order. For compression strains larger than $ecres, the residual stress is $fcres.
For compression strain, the slope of the unloading branch is defined by Equation 2. After reaching zero stress, the material reloads linearly to the point with the largest tensile strain that occurred before.
The tension envelope is linear until it reaches $ft. If the tension stiffening parameter $M is not specified, the tension envelope after reaching $ft is tri-linear and passes through the points ($etint, $ftint) and ($etres, $ftres) in that order. For tensile strains larger than $etres, the residual stress is $fcres.
If $M is specified, the nonlinear tension stiffening behavior defined by Equation 3. It is suggested that $M = (75 mm)*ρl/db where ρl is the steel ratio in the direction parallel to the material direction and db is the bar diameter in mm.
The material unloads from tension strain using a slope of $Ec. After reaching zero stress, the material targets the point (0, -$alpha*$ft). Thereafter, the material loads linearly to the point where the peak compressive strain previously occurred. In the case where the slope leading to this target point is less than that for the point (0, -$alpha*$ft), the material reloads directly to the point where peak compressive strain occurred.
Biaxial Behavior
The ConcretewBeta material model accounts for the biaxial strain field on the concrete compressive behavior when used in conjunction with the Truss2 element. The Truss2 element computes the strain normal to the direction of the element (see Truss2 Element).
Figure 2 shows the relationship between concrete compressive stress reduction factor, β, and the normal tensile strain, εn. For compressive stresses, the instantaneous stress value computed by the material is β*fc where fc is the compressive stress given by the uniaxial behavior described above. For positive (tensile) stress, β = 1. For compressive stress, the β-εn relationship is tri-linear and passes through the points (0,1), ($ebint, $bint), and ($ebres, $bres) in that order. For normal tensile strains larger than $ebres, β = $bres.
Example
See: Truss Model Example - Squat RC Wall
References
Hoshikuma, J., Kawashima, K., Nagaya, K., and Taylor, A. W. (1997). “Stress-strain model for confined reinforced concrete in bridge piers.” Journal of Structural Engineering, 123(5), 624-633.
Lu, Y., and Panagiotou, M. (2013). “Three-Dimensional Nonlinear Cyclic Beam-Truss Model for Reinforced Concrete Non-Planar Walls.” Journal of Structural Engineering, published online.
Panagiotou, M., Restrepo, J.I., Schoettler, M., and Kim G. (2012). "Nonlinear cyclic truss model for reinforced concrete walls." ACI Structural Journal, 109(2), 205-214.
Stevens, N. J., Uzumeri, S. M., Collins, M. P., and Will, T. G. (1991). “Constitutive model for reinforced concrete finite element analysis.” ACI Structural Journal, 88(1), 49-59.
Code Developed by: Yuan Lu, UC Berkeley and Marios Panagiotou, UC Berkeley