Modified Ibarra-Medina-Krawinkler Deterioration Model with Pinched Hysteretic Response (ModIMKPinching Material)

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

This command is used to construct a ModIMKPinching material. This material simulates the modified Ibarra-Medina-Krawinkler deterioration model with pinching hysteretic response. NOTE: before you use this material make sure that you have downloaded the latest OpenSees version. A youtube video presents a summary of this model including the way to be used within openSees (http://youtu.be/YHBHQ-xuybE).

uniaxialMaterial ModIMKPinching $matTag $K0 $as_Plus $as_Neg $My_Plus $My_Neg $FprPos $FprNeg $A_pinch $Lamda_S $Lamda_C $Lamda_A $Lamda_K $c_S $c_C $c_A $c_K $theta_p_Plus $theta_p_Neg $theta_pc_Plus $theta_pc_Neg $Res_Pos $Res_Neg $theta_u_Plus $theta_u_Neg $D_Plus $D_Neg

---

$matTag	integer tag identifying material
$K0	elastic stiffness
$as_Plus	strain hardening ratio for positive loading direction
$as_Neg	strain hardening ratio for negative loading direction
$My_Plus	effective yield strength for positive loading direction
$My_Neg	effective yield strength for negative loading direction (Must be defined as a negative value)
$FprPos	Ratio of the force at which reloading begins to force corresponding to the maximum historic deformation demand (positive loading direction)
$FprNeg	Ratio of the force at which reloading begins to force corresponding to the absolute maximum historic deformation demand (negative loading direction)
$A_Pinch	Ratio of reloading stiffness
$Lamda_S	Cyclic deterioration parameter for strength deterioration [see definitions in Lignos and Krawinkler (2011)]
$Lamda_C	Cyclic deterioration parameter for post-capping strength deterioration [see definitions in Lignos and Krawinkler (2011)]
$Lamda_A	Cyclic deterioration parameter for acceleration reloading stiffness deterioration [see definitions in Lignos and Krawinkler (2011)]
$Lamda_K	Cyclic deterioration parameter for unloading stiffness deterioration [see definitions in Lignos and Krawinkler (2011)]
$c_S	rate of strength deterioration. The default value is 1.0.
$c_C	rate of post-capping strength deterioration. The default value is 1.0.
$c_A	rate of accelerated reloading deterioration. The default value is 1.0.
$c_K	rate of unloading stiffness deterioration. The default value is 1.0.
$theta_p_Plus	pre-capping rotation for positive loading direction (often noted as plastic rotation capacity)
$theta_p_Neg	pre-capping rotation for negative loading direction (often noted as plastic rotation capacity) (must be defined as a positive value)
$theta_pc_Plus	post-capping rotation for positive loading direction
$theta_pc_Neg	post-capping rotation for negative loading direction (must be defined as a positive value)
$Res_Pos	residual strength ratio for positive loading direction
$Res_Neg	residual strength ratio for negative loading direction (must be defined as a positive value)
$theta_u_Plus	ultimate rotation capacity for positive loading direction
$theta_u_Neg	ultimate rotation capacity for negative loading direction (must be defined as a positive value)
$D_Plus	rate of cyclic deterioration in the positive loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0.
$D_Neg	rate of cyclic deterioration in the negative loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0.

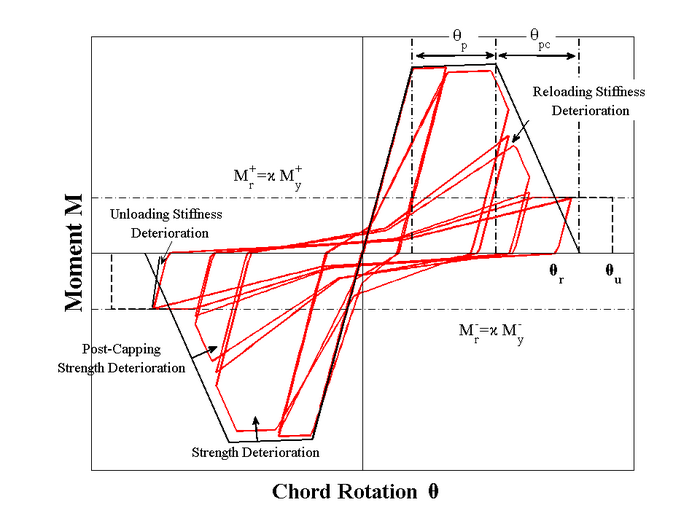
Image from: Lignos and Krawinkler (2012)

The deterioration model parameters can be calibrated based on actual experimental data of RC beams in terms of load - displacement or moment - rotation. Examples of such calibrations can be found in Lignos (2008) and Lignos and Krawinkler (2012).

---

References:

[1]	Lignos, D.G., Krawinkler, H. (2012). “Development and Utilization of Structural Component Databases for Performance-Based Earthquake Engineering", Journal of Structural Engineering, ASCE (accepted for publication).
[2]	Lignos, D.G., and Krawinkler, H. (2011). “Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading”, Journal of Structural Engineering, ASCE, Vol. 137 (11), 1291-1302.
[3]	Lignos, D.G. and Krawinkler, H. (2012). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Rep.No.TB 177, The John A. Blume Earthquake Engineering Research Center, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports]
[4]	Lignos, D.G. (2008). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Ph.D. Dissertation, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA.
[5]	Ibarra L.F., and Krawinkler, H. (2005). “Global collapse of frame structures under seismic excitations”, Rep. No. TB 152, The John A. Blume Earthquake Engineering Center, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports]
[6]	Ibarra L.F., Medina R. A., and Krawinkler H. (2005). “Hysteretic models that incorporate strength and stiffness deterioration”, Earthquake Engineering and Structural Dynamics, 34(12), 1489-1511.

Code Developed by : by Dr. Dimitrios G. Lignos, McGill University