Calibration of Maxwell Material

Example posted by: Dr. Dimitrios G. Lignos, McGill University

---

This example demonstrates how to conduct a calibration of a viscous damper using the maxwell model.

The files needed to analyze this structure in OpenSees are included here:

• The main file: Maxwell_Calibrator.tcl

Supporting procedure files

• SquareSsection.tcl – displays a square fiber section
• Damper.txt – contains the displacement loading history of the damper in units of mm

All files are available in a compressed format here: Calibration_Maxwell_example.zip

The rest of this example describes the model and shows the analysis results.

Model Description

File:Maxwell-Fig1.PNG

Figure 1. Schematic representation of a viscous damper.

The viscous damper is modeled with the nonlinearBeamColumn element. This element follow a Maxwell hysteretic response. An idealized schematic of the model is presented in Figure 1.

The units of the model are mm, N, and seconds.

Basic Geometry

The basic geometry of the viscous damper is defined by input variables for the length L=5000mm, and area A = 12000mm². Two nodes are used for the geometry of the damper.

Damper Section

A square section is used to define the area A of the damper (A_damper = 10000.0mm²).

Damper Links

nonlinearBeamColumn elements are used to link the two nodes that define the geometry of the viscous damper with n=5 sections of integration and the damper section defined previously.

Constraints

Node 1 is pinned. A roller is assigned to node 2

Maxwell Material

To model the viscous damper the Maxwell is used. The input parameters that are selected for the damper example are as follows: Axial Stiffness K = 500000.0 N/mm, Viscous Coefficient C=100000.0 N(s/mm)^0.30 and exponent a=0.30.

Loading

The viscous damper is loaded with a displacement history that is called Damper.txt in the axial loading direction. A linear pattern is selected and the node of application is Node 2.

Recorders

The recorders used in this example include:

• The localForce recorder to track the axial force of the viscous damper
• The stressStrain recorder to track the stress and strain history of the viscous damper in section 3.

Analysis

In order to calibrate the viscous damper a multiple support excitation option is selected with application of displacement as the imposed motion. This is necessary since an integration step dt should be specified for integration of strain histories for each time step.

Results

Comparison of OpenSees Models

Figure 3. Pushover Curve: Comparison of OpenSees Models

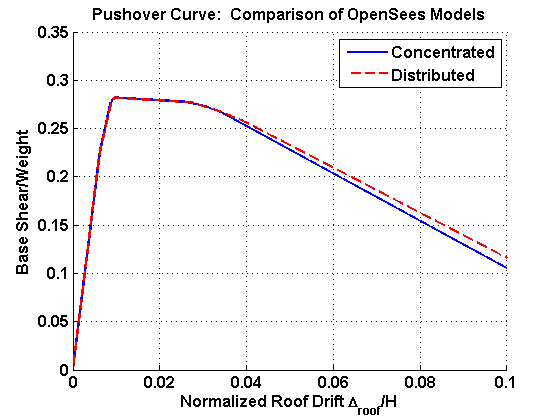
Theoretically, the results of the distributed plasticity model should approach those of the concentrated plasticity model as the length of the plastic hinge regions approaches zero. Because of localized instability due to the stress-strain formulation of the beam with hinges element, the distributed plasticity model does not give reasonable results when the length of the plastic hinge is very small (i.e., 10e^-5). Therefore, the length of the plastic hinges was increased from 10e^-5 until the results of this model approached those of the concentrated plasticity model. The plastic hinge length that led to agreement between the models was 0.4% of the frame member's total length. The periods of the concentrated and distributed models are very close: T₁ = 0.83 s (con) vs. 0.82 s (dist) and T₂ = 0.22 s (con) vs. 0.21 s (dist).

The results of the pushover analyses from the OpenSees models are shown in Figure 3. This figure shows the normalized base shear (weight of the structure divided by the base shear) versus the roof drift (roof displacement divided by the roof elevation). The models are nearly identical until about 2.5% roof drift when their curves begin to diverge. The descending branch of the the concentrated plasticity model is slightly steeper, but the two models agree reasonably well as there is less than 10% percent difference in the base shears at 10% roof drift.

References

1. Ibarra, L. F., and Krawinkler, H. (2005). “Global collapse of frame structures under seismic excitations,” Technical Report 152, The John A. Blume Earthquake Engineering Research Center, Department of Civil Engineering, Stanford University, Stanford, CA. [electronic version: https://blume.stanford.edu/tech_reports]
2. Ibarra, L. F., Medina, R. A., and Krawinkler, H. (2005). “Hysteretic models that incorporate strength and stiffness deterioration,” Earthquake Engineering and Structural Dynamics, Vol. 34, 12, pp. 1489-1511.
3. Lignos, D. G., and Krawinkler, H. (2009). “Sidesway Collapse of Deteriorating Structural Systems under Seismic Excitations,” Technical Report 172, The John A. Blume Earthquake Engineering Research Center, Department of Civil Engineering, Stanford University, Stanford, CA.
4. Lignos, D. G., and Krawinkler, H. (2010). “Deterioration Modeling of Steel Beams and Columns in Support to Collapse Prediction of Steel Moment Frames,” ASCE, Journal of Structural Engineering (under review).