ZeroLengthContactNTS2D: Difference between revisions
No edit summary |
No edit summary |
||
| Line 35: | Line 35: | ||
EXAMPLE: | EXAMPLE: | ||
[ | [[File:zeroLengthContactNTS2D _fig1.jpg]] | ||
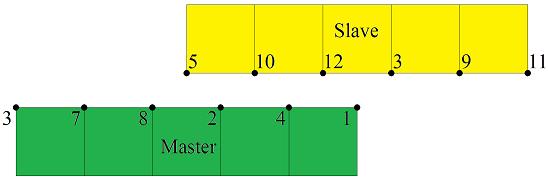
element zeroLengthContactNTS2D 1 -sNdNum 6 -mNdNum 6 - Nodes 5 10 12 3 9 11 1 4 2 8 7 1e8 1e8 16 | element zeroLengthContactNTS2D 1 -sNdNum 6 -mNdNum 6 - Nodes 5 10 12 3 9 11 1 4 2 8 7 1e8 1e8 16 | ||
Revision as of 22:32, 21 January 2010
This command is used to construct a zeroLengthContactNTS2D element object. This is a Node-To-Segment (NTS) frictional contact element used in two dimensional analysis for contact between elements with 2 DOF nodes.
| element zeroLengtContactNTS2Dh $eleTag -sNdNum $sNdNum -mNdNum $mNdNum -Nodes $Nodes $Kn $kt $phi |
| $eleTag | unique element object tag |
| $sNdNum | Number of Slave Nodes |
| $mNdNum | Number of Master nodes |
| $Nodes ... | Slave and master node tags respectively |
| $Kn | Penalty in normal direction |
| $Kt | Penalty in tangential direction |
| $phi | Friction angle in degrees |
NOTES:
- The contact element is node-to-segment (NTS) contact. The relation follows Mohr-Coulomb frictional law: <math>T = N tan(\phi)</math>, where T is the tangential force, N is normal force across the interface and ,math>\phi</math> is friction angle.
- For 2D contact, slave nodes and master nodes must be 2 DOF and notice that the slave and master nodes must be entered in counterclockwise order.
- The resulting tangent from the contact element is non-symmetric. Switch to the non-symmetric matrix solver if convergence problem is experienced.
- As opposed to node-to-node contact, predefined normal vector for node-to-segment (NTS) element is not required because contact normal will be calculated automatically at each step.
- contact element is implemented to handle large deformations.
EXAMPLE:
element zeroLengthContactNTS2D 1 -sNdNum 6 -mNdNum 6 - Nodes 5 10 12 3 9 11 1 4 2 8 7 1e8 1e8 16
Example 1:
This example simply shows the two quadrilateral elements in normal contact. The top element is in normal downward uniform force. The Tcl script of this example can be found here.
[image needed here]
Example 2:
This example shows two cantilever beams in contact. The beams were modeled using four-node quadrilateral elements and the end of top beam was subjected to a linearly increasing displacement. The Tcl scripts for this example can be found here.
[image needed here]
The following Figure shows the deflections of the two beams.
[image needed here]
REFERENCES:
- P. Wriggers, V.T. Vu and E. Stein, Finite-element formulation of large deformation impact–contact problems with friction, Comput. Struct. 37 (1990), pp. 319–331.
- Peter Wriggers. Computational Contact Mechanics. John Wiley & Sons Ltd. Chichester, 2002.
Code Developed by: R.G. Mikola, UC Berkeley and N. Sitar, UC Berkeley