Steel01 Material: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{CommandManualMenu}} | |||
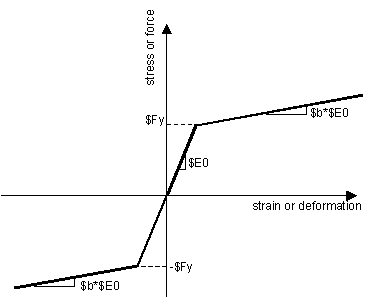
This command is used to construct a uniaxial bilinear steel material object with kinematic hardening and optional isotropic hardening described by a non-linear evolution equation (REF: Fedeas). | This command is used to construct a uniaxial bilinear steel material object with kinematic hardening and optional isotropic hardening described by a non-linear evolution equation (REF: Fedeas). | ||
Revision as of 21:07, 3 March 2010
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
This command is used to construct a uniaxial bilinear steel material object with kinematic hardening and optional isotropic hardening described by a non-linear evolution equation (REF: Fedeas).
| uniaxialMaterial Steel01 $matTag $Fy $E0 $b <$a1 $a2 $a3 $a4> |
| $matTag | integer tag identifying material |
| $Fy | yield strength |
| $E0 | initial elastic tangent |
| $b | strain-hardening ratio (ratio between post-yield tangent and initial elastic tangent) |
| $a1 | isotropic hardening parameter, increase of compression yield envelope as proportion of yield strength after a plastic strain of $a2*($Fy/E0). (optional) |
| $a2 | isotropic hardening parameter (see explanation under $a1). (optional). |
| $a3 | isotropic hardening parameter, increase of tension yield envelope as proportion of yield strength after a plastic strain of $a4*($Fy/E0). (optional) |
| $a4 | isotropic hardening parameter (see explanation under $a3). (optional) |
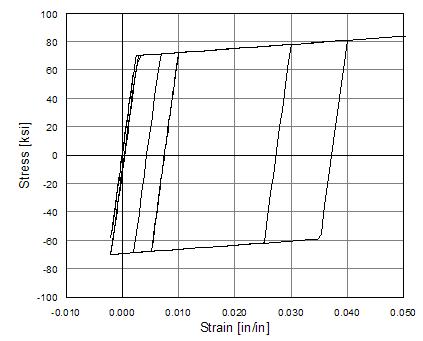
Steel01 Material -- Hysteretic Behavior of Model w/o Isotropic Hardening
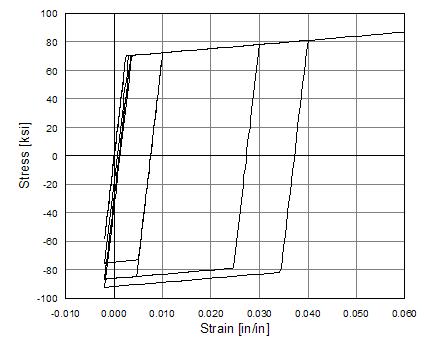
Steel01 Material -- Hysteretic Behavior of Model with Isotropic Hardening in Compression
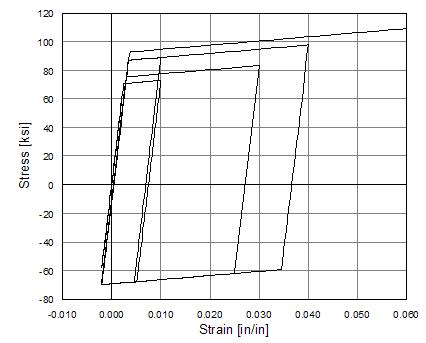
Steel01 Material -- Hysteretic Behavior of Model with Isotropic Hardening in Tension
Code Developed by: Filip Filippou, UC Berkeley
Images Developed by: Silvia Mazzoni