KikuchiBearing Element: Difference between revisions
No edit summary |
No edit summary |
||
| Line 29: | Line 29: | ||
| '''$limDisp''' || minimum deformation to calculate equivalent coefficient of MSS (see note 1) | | '''$limDisp''' || minimum deformation to calculate equivalent coefficient of MSS (see note 1) | ||
|- | |- | ||
| '''$nMNS''' || number of springs in MNS = nMNS*nMNS | | '''$nMNS''' || number of springs in MNS = nMNS*nMNS (for round and square shape) | ||
|- | |- | ||
| '''$matMNSTag''' || matTag for MNS | | '''$matMNSTag''' || matTag for MNS | ||
| Line 52: | Line 52: | ||
NOTES: | NOTES: | ||
1) If '''$ | 1) If '''$limdisp''' is positive and the shear deformation of MSS exceeds '''$limdisp''', | ||
this element calculates equivalent coefficient to adjust force and stiffness of MSS. | this element calculates equivalent coefficient to adjust force and stiffness of MSS. | ||
The adjusted MSS force and stiffness reproduce the behavior of the previously defined uniaxial material | The adjusted MSS force and stiffness reproduce the behavior of the previously defined uniaxial material | ||
under monotonic loading in every direction. | under monotonic loading in every direction. | ||
2) Recommended value is (D/t)*sqrt(3*G/K), where D, t, G and K are size, thickness, shear modulus and bulk modulus of a rubber layer, respectively. | 2) Recommended value is (D/t)*sqrt(3*G/K), where D, t, G and K are size (for round and square shape), thickness, shear modulus and bulk modulus of a rubber layer, respectively. | ||
3) The valid queries to a | 3) The valid queries to a KikuchiBearing element when creating an ElementRecorder object are | ||
'globalForce', 'localForce', 'basicForce', 'localDisplacement' and 'basicDeformation'. | 'globalForce', 'localForce', 'basicForce', 'localDisplacement' and 'basicDeformation'. | ||
Revision as of 14:08, 1 June 2014
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
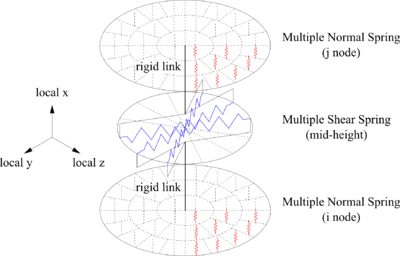
This command is used to construct a KikuchiBearing element object, which is defined by two nodes. This element consists of multiple shear spring model (MSS) and multiple normal spring model (MNS).
| element KikuchiBearing $eleTag $iNode $jNode -shape $shape -size $size $totalRubber <-totalHeight $totalHeight> -nMSS $nMSS -matMSS $matMSSTag <-limDisp $limDisp> -nMNS $nMNS -matMNS $matMNSTag <-lambda $lambda> <-orient <$x1 $x2 $x3> $yp1 $yp2 $yp3> <-mass $m> <-noPDInput> <-noTilt> <-adjustPDOutput $ci $cj> <-doBalance $limFo $limFi $nIter> |
| $eleTag | unique element object tag |
| $inode $jnode | end nodes |
| $shape | following shapes are available: round, square |
| $size | diameter (round shape), length of edge (square shape) |
| $totalRubber | total rubber thickness |
| $totalHeight | total height of the bearing (defaulut: distance between iNode and jNode) |
| $nMSS | number of springs in MSS = nMSS |
| $matMSSTag | matTag for MSS |
| $limDisp | minimum deformation to calculate equivalent coefficient of MSS (see note 1) |
| $nMNS | number of springs in MNS = nMNS*nMNS (for round and square shape) |
| $matMNSTag | matTag for MNS |
| $lambda | parameter to calculate compression modulus distribution on MNS (see note 2) |
| $x1 $x2 $x3 | vector components in global coordinates defining local x-axis |
| $yp1 $yp2 $yp3 | vector components in global coordinates defining vector yp which lies in the local x-y plane for the element |
| $m | element mass |
| -noPDInput | not consider P-Delta moment |
| -noTilt | not consider tilt of rigid link |
| $ci $cj | P-Delta moment adjustment for reaction force (default: $ci=0.5, $cj=0.5) |
| $limFo $limFi $nIter | tolerance of external unbalanced force ($limFo), tolorance of internal unbalanced force ($limFi), number of iterations to get rid of internal unbalanced force ($nIter) |
NOTES:
1) If $limdisp is positive and the shear deformation of MSS exceeds $limdisp, this element calculates equivalent coefficient to adjust force and stiffness of MSS. The adjusted MSS force and stiffness reproduce the behavior of the previously defined uniaxial material under monotonic loading in every direction.
2) Recommended value is (D/t)*sqrt(3*G/K), where D, t, G and K are size (for round and square shape), thickness, shear modulus and bulk modulus of a rubber layer, respectively.
3) The valid queries to a KikuchiBearing element when creating an ElementRecorder object are 'globalForce', 'localForce', 'basicForce', 'localDisplacement' and 'basicDeformation'.
EXAMPLE:
element KikuchiBearing 1 1 2 -shape round -size 1.016 0.320 -nMSS 8 -matMSS 1 -nMNS 30 -matMNS 2
KikuchiBearing_Sample.tcl, KikuchiBearing_input_Z.tcl, KikuchiBearing_input_X.tcl
| case 1: P-Delta effect not considered (use -noPDInput -noTilt option) |
| case 2: P-Delta effect considered, uniform distribution of compression modulus |
| case 3: P-Delta effect considered (use -lambda option) |
REFERENCES:
M. Kikuchi , I. D. Aiken and A. Kasalanati , "Simulation analysis for the ultimate behavior of full-scale lead-rubber seismic isolation bearings", 15th World Conference on Earthquake Engineering, No. 1688, 2012.