Linear Transformation: Difference between revisions

From OpenSeesWiki
Jump to navigation Jump to search
No edit summary
(Description of offsets was incorrect)
 
(10 intermediate revisions by 2 users not shown)
Line 27: Line 27:
These items need to be specified for the three-dimensional problem.
These items need to be specified for the three-dimensional problem.
|-
|-
|  '''$dXi $dYi $dZi''' || joint offset values -- offsets specified with respect to the global coordinate system for element-end node i (the number of arguments depends on the dimensions of the current model). The offset vector is is oriented from node i to node j as shown in a figure below. (optional)
|  '''$dXi $dYi $dZi''' || joint offset values -- offsets specified with respect to the global coordinate system for element-end node i (optional, the number of arguments depends on the dimensions of the current model).  
|-
|-
| ''' $dXj $dYj $dZj''' || joint offset values -- offsets specified with respect to the global coordinate system for element-end node j (the number of arguments depends on the dimensions of the current model). The offset vector is is oriented from node i to node j as shown in a figure below. (optional)
| ''' $dXj $dYj $dZj''' || joint offset values -- offsets specified with respect to the global coordinate system for element-end node j (optional, the number of arguments depends on the dimensions of the current model).  
|}
|}
A refresher on Euclidean Geometry and Coordinate Systems:
A single vector may be defined by two points. It has length, direction, and location in
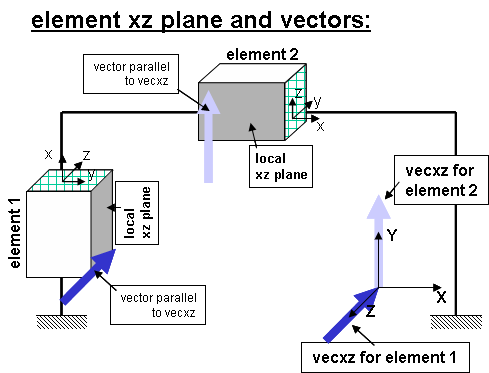
space. When this vector is used to define a coordinate axis, only its direction is important. Now any 2 vectors, Vr and Vs, not parallel, define a plane that is parallel to them both. The cross-product of these vectors define a third vector, Vt, that is perpendicular to both Vr and Vs and hence normal to the plane: Vt = Vr X Vs.




The element coordinate system is specified as follows:
The element coordinate system is specified as follows:


The x-axis is the axis connecting the two element nodes; the y- and z-axes are then defined using a vector that lies on a plane parallel to the local x-z plane -- vecxz. The local y-axis is defined by taking the cross product of the vecxz vector and the x-axis.. The section is attached to the element such that the y-z coordinate system used to specify the section corresponds to the y-z axes of the element.
The x-axis is a vector given by the two element nodes; The vector vecxz is a vector the user specifies that must not be parallel to the x-axis. The x-axis along with the vecxz Vector define the xz plane. The local y-axis is defined by taking the cross product of the x-axis vector and the vecxz vector (Vy = Vxz X Vx). The local z-axis is then found simply by taking the cross product of the y-axis and x-axis vectors (Vz = Vx X Vy). The section is attached to the element such that the y-z coordinate system used to specify the section corresponds to the y-z axes of the element.
    
    


Line 43: Line 50:




NOTE: When in 2D, local x and y axes are in the X-Y plane, where X and Y are global axes. Local x axis is the axis connecting the two element nodes, and local y and z axes follow the right-hand rule (e.g., if the element is aligned with the positive Y axis, the local y axis is aligned with the positive X axis, and if the element is aligned with the positive X axis, the local y axis is aligned with the positive Y axis). Orientation of local y and z axes is important for definition of the fiber section.
NOTE: When in 2D, local x and y axes are in the X-Y plane, where X and Y are global axes. Local x axis is the axis connecting the two element nodes, and local y and z axes follow the right-hand rule (e.g., if the element is aligned with the positive Y axis, the local y axis is aligned with the negative X axis, and if the element is aligned with the positive X axis, the local y axis is aligned with the positive Y axis). Orientation of local y and z axes is important for definition of the fiber section.
----
----


Line 59: Line 66:
#Element 2 : tag 2 : vecxZ = y axis
#Element 2 : tag 2 : vecxZ = y axis
geomTransf Linear 2 0 1 0
geomTransf Linear 2 0 1 0
#If there was a rigid offset at the top of element 1:
geomTransf Linear 1 0 0 -1 -jntOffset 0.0 0.0 0.0 0.0 -$Offset 0.0




Latest revision as of 20:57, 19 November 2020



This command is used to construct a linear coordinate transformation (LinearCrdTransf) object, which performs a linear geometric transformation of beam stiffness and resisting force from the basic system to the global-coordinate system.

For a two-dimensional problem:

geomTransf Linear $transfTag <-jntOffset $dXi $dYi $dXj $dYj>

For a three-dimensional problem:

geomTransf Linear $transfTag $vecxzX $vecxzY $vecxzZ <-jntOffset $dXi $dYi $dZi $dXj $dYj $dZj>


$transfTag integer tag identifying transformation
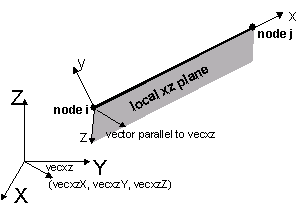
$vecxzX $vecxzY $vecxzZ X, Y, and Z components of vecxz, the vector used to define the local x-z plane of the local-coordinate system. The local y-axis is defined by taking the cross product of the vecxz vector and the x-axis.

These components are specified in the global-coordinate system X,Y,Z and define a vector that is in a plane parallel to the x-z plane of the local-coordinate system.

These items need to be specified for the three-dimensional problem.

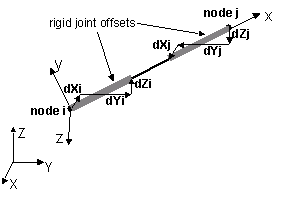
$dXi $dYi $dZi joint offset values -- offsets specified with respect to the global coordinate system for element-end node i (optional, the number of arguments depends on the dimensions of the current model).
$dXj $dYj $dZj joint offset values -- offsets specified with respect to the global coordinate system for element-end node j (optional, the number of arguments depends on the dimensions of the current model).


A refresher on Euclidean Geometry and Coordinate Systems:

A single vector may be defined by two points. It has length, direction, and location in space. When this vector is used to define a coordinate axis, only its direction is important. Now any 2 vectors, Vr and Vs, not parallel, define a plane that is parallel to them both. The cross-product of these vectors define a third vector, Vt, that is perpendicular to both Vr and Vs and hence normal to the plane: Vt = Vr X Vs.


The element coordinate system is specified as follows:

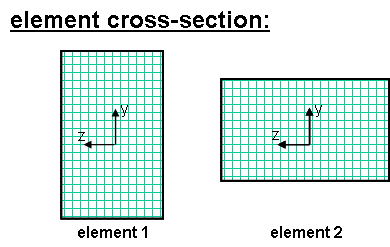
The x-axis is a vector given by the two element nodes; The vector vecxz is a vector the user specifies that must not be parallel to the x-axis. The x-axis along with the vecxz Vector define the xz plane. The local y-axis is defined by taking the cross product of the x-axis vector and the vecxz vector (Vy = Vxz X Vx). The local z-axis is then found simply by taking the cross product of the y-axis and x-axis vectors (Vz = Vx X Vy). The section is attached to the element such that the y-z coordinate system used to specify the section corresponds to the y-z axes of the element.



NOTE: When in 2D, local x and y axes are in the X-Y plane, where X and Y are global axes. Local x axis is the axis connecting the two element nodes, and local y and z axes follow the right-hand rule (e.g., if the element is aligned with the positive Y axis, the local y axis is aligned with the negative X axis, and if the element is aligned with the positive X axis, the local y axis is aligned with the positive Y axis). Orientation of local y and z axes is important for definition of the fiber section.

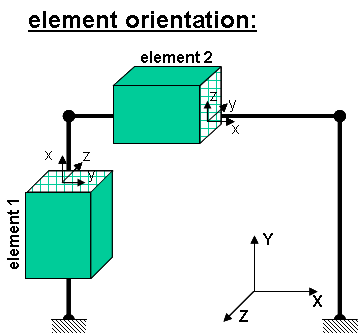
EXAMPLE:

  1. Element 1 : tag 1 : vecxZ = zaxis

geomTransf Linear 1 0 0 -1

  1. Element 2 : tag 2 : vecxZ = y axis

geomTransf Linear 2 0 1 0

  1. If there was a rigid offset at the top of element 1:

geomTransf Linear 1 0 0 -1 -jntOffset 0.0 0.0 0.0 0.0 -$Offset 0.0


Code Developed by: Remo Magalhaes de Souza

Images Developed by: Silvia Mazzoni

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=Linear_Transformation&oldid=12790"