RambergOsgoodSteel Material: Difference between revisions

From OpenSeesWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(19 intermediate revisions by the same user not shown)
Line 4: Line 4:


{|     
{|     
  | style="background:yellow; color:black; width:800px " | '''uniaxialMaterial RambergOsgoodSteel $matTag $fy $Es $a $n'''   
  | style="background:yellow; color:black; width:800px " | '''uniaxialMaterial RambergOsgoodSteel $matTag $fy $E0 $a $n'''   
  |}   
  |}   
      
      
Line 22: Line 22:
|  '''$n''' || Parameters to control the transition from elastic to plastic branches. And controls the hardening of the material by increasing the "n" hardening ratio will be decreased.
|  '''$n''' || Parameters to control the transition from elastic to plastic branches. And controls the hardening of the material by increasing the "n" hardening ratio will be decreased.


:Commonly used values for $n are ~5 or greater. ($n must be odd number).
:Commonly used values for $n are ~5 or greater.
|}
|}
----
----
Line 28: Line 28:
'''Introduction to the Ramberg–Osgood’s Material Model:'''
'''Introduction to the Ramberg–Osgood’s Material Model:'''


In earthquake engineering, Ramberg–Osgood functions are often used to model the behavior of structural steel materials and components. These functions are obtained when the power is normalized to an arbitrary strain, ε0, for which the plastic component of the strain, εplastic, is not zero. Generally the yield strain, εy, provides a good choice for normalization of strain, the Ramberg–Osgood function is expressed as:
In earthquake engineering, Ramberg–Osgood functions are often used to model the behavior of structural steel materials and components. These functions are obtained when the power is normalized to an arbitrary strain, ε0, for which the plastic component of the strain, εplastic, is not zero. Generally the yield strain, εy, provides a good choice for normalization of strain, the Ramberg–Osgood function is expressed as [1]:
<math>\varepsilon = \sigma/E + a(\sigma/\sigma_0)^n</math>
 
[[File:RambergOsgoodSteel04.png|200px|center]]
 
Where E0 is the initial elastic modulus and σ0 is equal to Eε0.
----
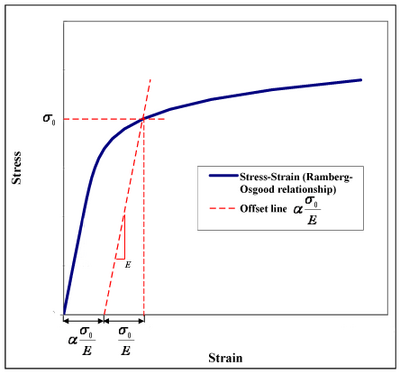
'''More explanation about parameter “a” (yielding offset)'''
 
The value “a” which is equal to ασ/E_0  can be seen as a yield offset, as shown in Fig.1. This comes from the fact that
 
[[File:RambergOsgoodSteel05.png|200px|center]]
 
 
when σ=σ0.
 
 
Accordingly (see Fig.1):
 
[[File:RambergOsgoodSteel03.png|400px|center]]
 
Values for α can also be found by means of fitting to experimental data, although for some materials, it can be fixed in order to have the yield offset equal to the accepted value of strain of 0.2%, which means [2]:
[[File:RambergOsgoodSteel06.png|100px|center]]
 
 
[[File:RambergOsgoodSteel02.png|400px|thumb|center|Fig. 1: Generic representation of the Stress-Strain curve by means of the Ramberg–Osgood equation. Strain corresponding to the yield point is the sum of the elastic and plastic components.]]
 
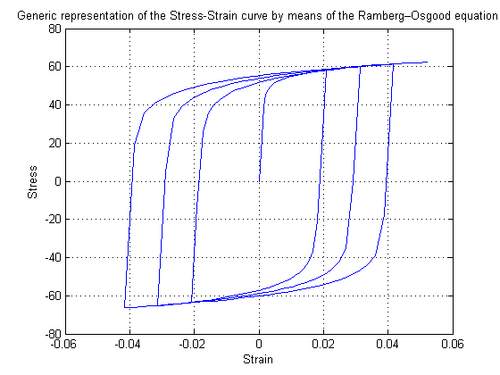
[[File:RambergOsgoodSteel01.png|500px|thumb|center|Fig. 2: RambergOsgoodSteel Material -- Hysteretic Behavior of Model]]
 
----
'''REFERENCE:'''
[1] Michel Bruneau , Chia-Ming Uang Andrew Whittaker. “Ductile Design of Steel Structures” McGraw-Hill Professional, 1997, ISBN: 0070085803 - 978-0070085800
[2] Ramberg, W., & Osgood, W. R. (1943). “Description of stress-strain curves by three parameters.” Technical Note No. 902, National Advisory Committee For Aeronautics, Washington DC.
----
'''Contact Authors:'''
 
Reza Rahimi, Graduate Research Assistant of Structural Engineering,  Dalhousie University, reza.rahimi@dal.ca
 
Reza Sepasdar, Graduate Research Assistant of Structural Engineering,  Dalhousie University, reza.sepasdar@dal.ca
 
Mohammad Reza Banan, Associate Professor of Civil Engineering, Department of Civil and Environmental Engineering, Shiraz University, Shiraz, Iran, banan@shirazu.ac.ir

Latest revision as of 13:02, 26 July 2016



This command is used to construct a Ramberg–Osgood steel material object.

uniaxialMaterial RambergOsgoodSteel $matTag $fy $E0 $a $n
$matTag integer tag identifying material
$fy yield strength
$E0 initial elastic tangent
$a “yield offset” and the Commonly used value for $a is 0.002
$n Parameters to control the transition from elastic to plastic branches. And controls the hardening of the material by increasing the "n" hardening ratio will be decreased.
Commonly used values for $n are ~5 or greater.

Introduction to the Ramberg–Osgood’s Material Model:

In earthquake engineering, Ramberg–Osgood functions are often used to model the behavior of structural steel materials and components. These functions are obtained when the power is normalized to an arbitrary strain, ε0, for which the plastic component of the strain, εplastic, is not zero. Generally the yield strain, εy, provides a good choice for normalization of strain, the Ramberg–Osgood function is expressed as [1]:

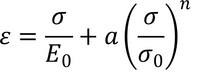
Where E0 is the initial elastic modulus and σ0 is equal to Eε0.

More explanation about parameter “a” (yielding offset)

The value “a” which is equal to ασ/E_0 can be seen as a yield offset, as shown in Fig.1. This comes from the fact that


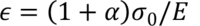
when σ=σ0.


Accordingly (see Fig.1):

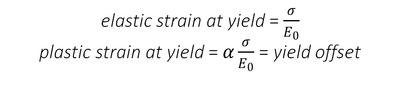
Values for α can also be found by means of fitting to experimental data, although for some materials, it can be fixed in order to have the yield offset equal to the accepted value of strain of 0.2%, which means [2]:


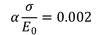
Fig. 1: Generic representation of the Stress-Strain curve by means of the Ramberg–Osgood equation. Strain corresponding to the yield point is the sum of the elastic and plastic components.
Fig. 2: RambergOsgoodSteel Material -- Hysteretic Behavior of Model

REFERENCE: 

[1] Michel Bruneau , Chia-Ming Uang Andrew Whittaker. “Ductile Design of Steel Structures” McGraw-Hill Professional, 1997, ISBN: 0070085803 - 978-0070085800
[2] Ramberg, W., & Osgood, W. R. (1943). “Description of stress-strain curves by three parameters.” Technical Note No. 902, National Advisory Committee For Aeronautics, Washington DC.

Contact Authors:

Reza Rahimi, Graduate Research Assistant of Structural Engineering, Dalhousie University, reza.rahimi@dal.ca

Reza Sepasdar, Graduate Research Assistant of Structural Engineering, Dalhousie University, reza.sepasdar@dal.ca

Mohammad Reza Banan, Associate Professor of Civil Engineering, Department of Civil and Environmental Engineering, Shiraz University, Shiraz, Iran, banan@shirazu.ac.ir

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=RambergOsgoodSteel_Material&oldid=12306"