Elastic Frame Example: Difference between revisions

From OpenSeesWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(9 intermediate revisions by the same user not shown)
Line 1: Line 1:
__NOTOC__
__NOTOC__
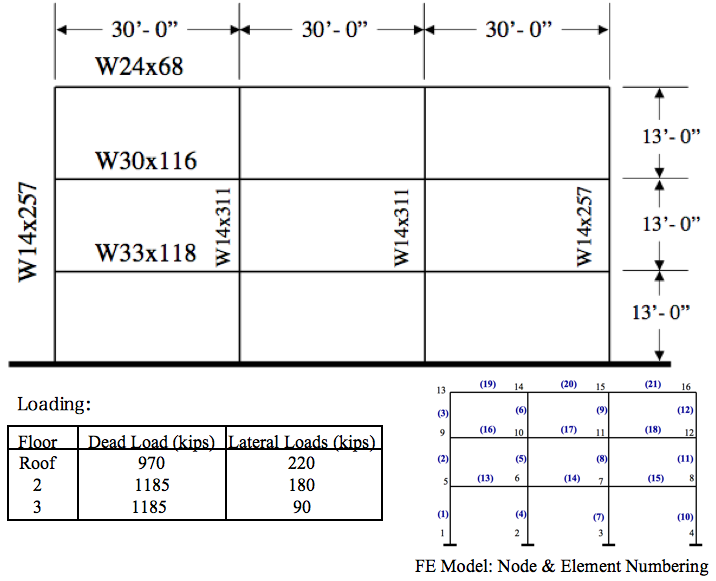
This example is of an elastic frame structure, as shown in the figure, subject to static loads. Here is the file: [[Media:ElasticFrame.tcl | ElasticFrame.tcl]]
This example is of an elastic frame structure, as shown in the figure, subject to static loads. '''Here is the file: [[Media:ElasticFrame.tcl | ElasticFrame.tcl]]'''


[[Image:ElasticFrame.png|link=Elastic Frame Example]]
[[Image:ElasticFrame.png|link=Elastic Frame Example]]
Line 7: Line 7:
# The lines in the dashed boxes are lines that appear in the input file.
# The lines in the dashed boxes are lines that appear in the input file.
#all lines that begin with '''#''' are comments, they are ignored by the program (interpreter) but are useful for documenting the code. When creating your own input scripts you are '''highly encouraged''' to use comments.
#all lines that begin with '''#''' are comments, they are ignored by the program (interpreter) but are useful for documenting the code. When creating your own input scripts you are '''highly encouraged''' to use comments.
# For brevity it is possible to put the comment after the command by using the ''';''' to signify end of a command.
# The printing of info to the screen makes this example more complicated than it needs to be. If you don't understand it, you can ignore it for now.


=== Parameters ===
=== Parameters ===


Before we build the model we are going to set some parameters using tcl variables and expression evaluation. We are going to set variables for PI, the gravtational constant g, and variables for each of our floor masses.
Before we build the model we are going to set some parameters using tcl variables and expression evaluation. We are going to set variables for PI, the gravtational constant g, and variables for each of our floor masses. We
are using the tcl '''set''' and '''expr''' commands.


<pre>
<pre>
Line 17: Line 20:
set ft  12.0
set ft  12.0
set m1  [expr 1185.0/(4*$g)]; # 4 nodes per floor                                                   
set m1  [expr 1185.0/(4*$g)]; # 4 nodes per floor                                                   
set m2  [expr 1185.0/(2.0*4*$g)]
set m2  [expr 1185.0/(4*$g)]
set m3  [expr  970.0/(2.0*4*$g)]
set m3  [expr  970.0/(4*$g)]
set w1  [expr 1185.0/(90*$ft)]
set w1  [expr 1185.0/(90*$ft)]
set w2  [expr 1185.0/(90*$ft)]
set w2  [expr 1185.0/(90*$ft)]
set w3  [expr  970.0/(90*$ft)]
set w3  [expr  970.0/(90*$ft)]
</pre>
</pre>


=== Model ===
=== Model ===
The model consists of sixteen nodes, twenty one elastic beam-column elements, a single load pattern with distributed loads, and constraints totally fixing the nodes at the base of the building. There are no material objects associated with the elastic elements, but there are geometric transformations. For this example all the columns have a PDelta transformation, and all the beams a linear transformation.
The model consists of sixteen nodes, twenty one elastic beam-column elements, a single load pattern with distributed loads, and constraints totally fixing the nodes at the base of the building. There are no material objects associated with the elastic elements, but there are geometric transformations. For this example all the columns have a PDelta transformation, and all the beams a linear transformation.


<pre>
<pre>
Line 103: Line 106:
     eleLoad -ele 19 20 21 -type -beamUniform -$w3
     eleLoad -ele 19 20 21 -type -beamUniform -$w3
}
}
</pre>
</pre>


=== Analysis - Gravity Load===
=== Analysis - Gravity Load===


We will now show the commands to perform a gravity load analysis. As the model is elastic we will use a Linear solution algorithm and use a single step of load control to get us to the desired load level.
We will now show the commands to perform a gravity load analysis. As the model is elastic we will use a Linear solution algorithm and use a single step of load control to get us to the desired load level.


<pre>
<pre>
Line 143: Line 145:
=== Print Info to Screen to Allow User to Check Results ===
=== Print Info to Screen to Allow User to Check Results ===


In addition to using recorders, it is possible to specify output using the print and puts commands. When no file identifiers are provided, these commands will print results to the screen.
In addition to using recorders, it is possible to specify output using the print and puts commands. When no file identifiers are provided, these commands will print results to the screen. We use the '''nodeReaction''' command to return the reactions at the individual nodes and the tcl '''lindex''' command to obtain the values from these lists.


<pre>
<pre>
Line 154: Line 156:
set node4Rxn [nodeReaction 4]
set node4Rxn [nodeReaction 4]


set inputedFy  [expr $Load1+$Load2+$Load3]
set inputedFy  [expr -$Load1-$Load2-$Load3]; # loads added negative Fy direction to ele           
set computedFx [expr [lindex $node1Rxn 0]+[lindex $node2Rxn 0]+[lindex $node3Rxn 0]+[lindex $node4Rxn 0]]
set computedFy [expr [lindex $node1Rxn 1]+[lindex $node2Rxn 1]+[lindex $node3Rxn 1]+[lindex $node4Rxn 1]]
 
puts "\nEqilibrium Check After Gravity:"
puts "SumX: Inputed: 0.0 + Computed: $computedFx = [expr 0.0+$computedFx]"
puts "SumY: Inputed: $inputedFy + Computed: $computedFy = [expr $inputedFy+$computedFy]"
</pre>
 
 
=== Add Lateral Loads ===
 
Now we prepare to add our lateral loads to the model. First we need to '''set the gravity loads acting constant''', i.e. we do not want them changing as we apply more loads to the model. Then we will create
load pattern with nodal loads to add to the model.
 
<pre>
# set gravity loads constant and time in domain to 0.0                                         
loadConst -time 0.0
 
timeSeries Linear 2
pattern Plain 2 2 {
    load 13 220.0 0.0 0.0
    load  9 180.0 0.0 0.0
    load  5  90.0 0.0 0.0
}
</pre>
 
 
=== Recorder ===
 
We will create an element recorder to record the forces at the bottom story columns.
 
<pre>
recorder Element -file eleForces.out -ele 1 4 7 10 forces
</pre>
 
 
=== Perform The Lateral Load Analysis ===
 
After the objects for the model, analysis and output has been defined we now perform the analysis.
 
<pre>
analyze 1
</pre>
 
 
=== Print Info to Screen to Allow User to Check Results ===
 
In addition to using recorders, it is possible to specify output using the print and puts commands. When no file identifiers are provided, these commands will print results to the screen.
 
<pre>
reactions
 
set node1Rxn [nodeReaction 1]; # nodeReaction command returns nodal reactions for specified node in a list     
set node2Rxn [nodeReaction 2]
set node3Rxn [nodeReaction 3]
set node4Rxn [nodeReaction 4]
 
set inputedFx  [expr 220.0+180.0+90.0]
set computedFx [expr [lindex $node1Rxn 0]+[lindex $node2Rxn 0]+[lindex $node3Rxn 0]+[lindex $node4Rxn 0]]
set computedFx [expr [lindex $node1Rxn 0]+[lindex $node2Rxn 0]+[lindex $node3Rxn 0]+[lindex $node4Rxn 0]]
set computedFy [expr [lindex $node1Rxn 1]+[lindex $node2Rxn 1]+[lindex $node3Rxn 1]+[lindex $node4Rxn 1]]
set computedFy [expr [lindex $node1Rxn 1]+[lindex $node2Rxn 1]+[lindex $node3Rxn 1]+[lindex $node4Rxn 1]]


puts "\nEqilibrium Check:"
puts "\nEqilibrium Check After Lateral Loads:"
puts "SumX: Inputed: 0.0 versus Computed: $computedFx"
puts "SumX: Inputed: $inputedFx + Computed: $computedFx = [expr $inputedFx+$computedFx]"
puts "SumY: Inputed: $inputedFy versus Computed: $computedFy"
puts "SumY: Inputed: $inputedFy + Computed: $computedFy = [expr $inputedFy+$computedFy]"
 
# print ele information for columns at bottom
print ele 1 4 7 19
</pre>
 
 
=== Finally look at the eigenvalues ===
 
After the lateral load analysis has completed we will look at the period of the structure. To do this we use the eigenvalue command to obtain the eigenvalues. These are returned in a tcl '''list'''. From the list we obtain the eigenvalue for the mode using the tcl '''lindex''' command and use the '''expr''' command to determine the period.
 
<pre>
set eigenValues [eigen 5]
 
puts "\nEigenvalues:"
set eigenValue [lindex $eigenValues 0]
puts "T[expr 0+1] = [expr 2*$PI/sqrt($eigenValue)]"
set eigenValue [lindex $eigenValues 1]
puts "T[expr 1+1] = [expr 2*$PI/sqrt($eigenValue)]"
set eigenValue [lindex $eigenValues 2]
puts "T[expr 2+1] = [expr 2*$PI/sqrt($eigenValue)]"
set eigenValue [lindex $eigenValues 3]
puts "T[expr 3+1] = [expr 2*$PI/sqrt($eigenValue)]"
set eigenValue [lindex $eigenValues 4]
puts "T[expr 4+1] = [expr 2*$PI/sqrt($eigenValue)]"
 
# create a recorder to record eigenvalues at all free nodes
recorder Node -file eigenvector.out -nodeRange 5 16 -dof 1 2 3 eigen 0
 
# record the results into the file
record
</pre>
</pre>


=== Results ===
=== Results ===
Line 167: Line 258:
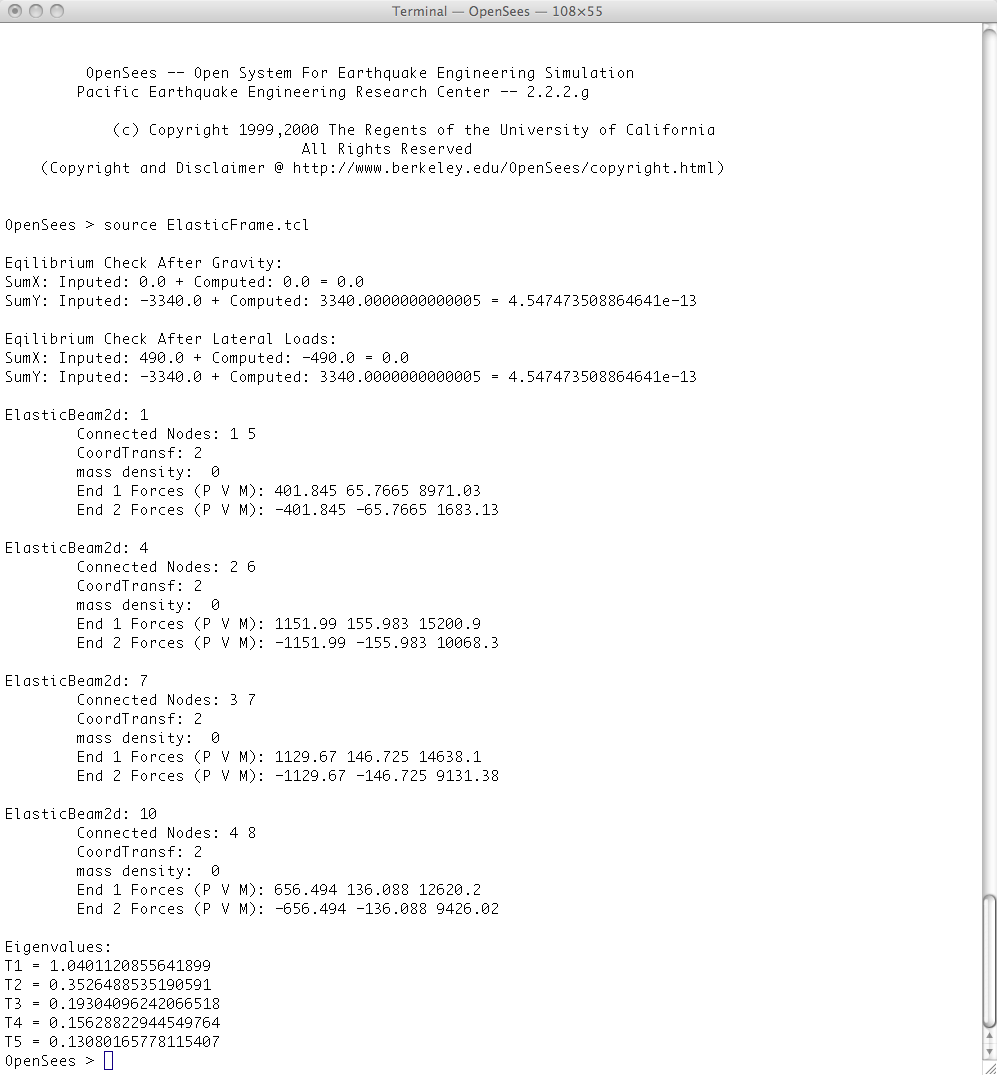
When you run this script, you should see the following printed to the screen:
When you run this script, you should see the following printed to the screen:


[[Image:TrussRun.png|link=Truss Run]]
[[Image:ElasticRun.png|link=Truss Run]]
 
In addition, your directory should contain the following 3 files with the data shown:

Latest revision as of 22:21, 15 March 2011

This example is of an elastic frame structure, as shown in the figure, subject to static loads. Here is the file: ElasticFrame.tcl

NOTE:

  1. The lines in the dashed boxes are lines that appear in the input file.
  2. all lines that begin with # are comments, they are ignored by the program (interpreter) but are useful for documenting the code. When creating your own input scripts you are highly encouraged to use comments.
  3. For brevity it is possible to put the comment after the command by using the ; to signify end of a command.
  4. The printing of info to the screen makes this example more complicated than it needs to be. If you don't understand it, you can ignore it for now.

Parameters

Before we build the model we are going to set some parameters using tcl variables and expression evaluation. We are going to set variables for PI, the gravtational constant g, and variables for each of our floor masses. We are using the tcl set and expr commands. 

set PI  [expr 2.0 * asin(1.0)]
set g   386.4
set ft  12.0
set m1  [expr 1185.0/(4*$g)]; # 4 nodes per floor                                                   
set m2  [expr 1185.0/(4*$g)]
set m3  [expr  970.0/(4*$g)]
set w1  [expr 1185.0/(90*$ft)]
set w2  [expr 1185.0/(90*$ft)]
set w3  [expr  970.0/(90*$ft)]


Model

The model consists of sixteen nodes, twenty one elastic beam-column elements, a single load pattern with distributed loads, and constraints totally fixing the nodes at the base of the building. There are no material objects associated with the elastic elements, but there are geometric transformations. For this example all the columns have a PDelta transformation, and all the beams a linear transformation. 

# Units: kips, in, sec
# Remove existing model                                                                                                       
wipe

# Create ModelBuilder (with two-dimensions and 3 DOF/node)   
model BasicBuilder -ndm 2 -ndf 3

                                                                                                           
# Create nodes & add to Domain - 
# command: node nodeId xCrd yCrd <-mass $massX $massY $massRz>                                 
#   NOTE: mass is optional                                           
node 1     0.0   0.0
node 2   360.0   0.0
node 3   720.0   0.0
node 4  1080.0   0.0
node 5    0.0  162.0 -mass $m1 $m1 0.0
node 6  360.0  162.0 -mass $m1 $m1 0.0
node 7  720.0  162.0 -mass $m1 $m1 0.0
node 8 1080.0  162.0 -mass $m1 $m1 0.0
node 9     0.0 324.0 -mass $m2 $m2 0.0
node 10  360.0 324.0 -mass $m2 $m2 0.0
node 11  720.0 324.0 -mass $m2 $m2 0.0
node 12 1080.0 324.0 -mass $m2 $m2 0.0
node 13    0.0 486.0 -mass $m3 $m3 0.0
node 14  360.0 486.0 -mass $m3 $m3 0.0
node 15  720.0 486.0 -mass $m3 $m3 0.0
node 16 1080.0 486.0 -mass $m3 $m3 0.0

# Set the boundary conditions - command: fix nodeID xResrnt? yRestrnt? rZRestrnt?    
fix 1 1 1 1
fix 2 1 1 1
fix 3 1 1 1
fix 4 1 1 1

# Define geometric transformations for beam-column elements                                     
geomTransf Linear 1; # beams                                                                    
geomTransf PDelta 2; # columns                  

# Define elements                                                                              
# Create elastic beam-column elements - 
# command: element elasticBeamColumn eleID node1 node2 A E Iz geomTransfTag                      

# Define the Columns                                                    
element elasticBeamColumn  1  1  5 75.6 29000.0 3400.0 2; # W14X257              
element elasticBeamColumn  2  5  9 75.6 29000.0 3400.0 2; # W14X257    
element elasticBeamColumn  3  9 13 75.6 29000.0 3400.0 2; # W14X257           
element elasticBeamColumn  4  2  6 91.4 29000.0 4330.0 2; # W14X311           
element elasticBeamColumn  5  6 10 91.4 29000.0 4330.0 2; # W14X311             
element elasticBeamColumn  6 10 14 91.4 29000.0 4330.0 2; # W14X311              
element elasticBeamColumn  7  3  7 91.4 29000.0 4330.0 2; # W14X311                 
element elasticBeamColumn  8  7 11 91.4 29000.0 4330.0 2; # W14X311                     
element elasticBeamColumn  9 11 15 91.4 29000.0 4330.0 2; # W14X311                  
element elasticBeamColumn 10  4  8 75.6 29000.0 3400.0 2; # W14X257         
element elasticBeamColumn 11  8 12 75.6 29000.0 3400.0 2; # W14X257                                          
element elasticBeamColumn 12 12 16 75.6 29000.0 3400.0 2; # W14X257                                     

# Define the Beams                                                                                   
element elasticBeamColumn 13  5  6 34.7 29000.0 5900.0 1; # W33X118        
element elasticBeamColumn 14  6  7 34.7 29000.0 5900.0 1; # W33X118        
element elasticBeamColumn 15  7  8 34.7 29000.0 5900.0 1; # W33X118                                          
element elasticBeamColumn 16  9 10 34.2 29000.0 4930.0 1; # W30X116                                           
element elasticBeamColumn 17 10 11 34.2 29000.0 4930.0 1; # W30X116                                          
element elasticBeamColumn 18 11 12 34.2 29000.0 4930.0 1; # W30X116                                             
element elasticBeamColumn 19 13 14 20.1 29000.0 1830.0 1; # W24X68                                            
element elasticBeamColumn 20 14 15 20.1 29000.0 1830.0 1; # W24X68                                          
element elasticBeamColumn 21 15 16 20.1 29000.0 1830.0 1; # W24X68 

# Create a Plain load pattern with a linear TimeSeries:                                        
#  command pattern Plain $tag $timeSeriesTag { $loads }                               
pattern Plain 1 1 {
    eleLoad -ele 13 14 15 -type -beamUniform -$w1
    eleLoad -ele 16 17 18 -type -beamUniform -$w2
    eleLoad -ele 19 20 21 -type -beamUniform -$w3
}


Analysis - Gravity Load

We will now show the commands to perform a gravity load analysis. As the model is elastic we will use a Linear solution algorithm and use a single step of load control to get us to the desired load level. 

# Create the system of equation
system BandSPD
    
# Create the DOF numberer, the reverse Cuthill-McKee algorithm
numberer RCM
    
# Create the constraint handler, a Plain handler is used as homo constraints
constraints Plain

# Create the integration scheme, the LoadControl scheme using steps of 1.0
integrator LoadControl 1.0

# Create the solution algorithm, a Linear algorithm is created
algorithm Linear

# create the analysis object 
analysis Static


Perform The Gravity Analysis

After the objects for the model, analysis and output has been defined we now perform the analysis. 

analyze 1


Print Info to Screen to Allow User to Check Results

In addition to using recorders, it is possible to specify output using the print and puts commands. When no file identifiers are provided, these commands will print results to the screen. We use the nodeReaction command to return the reactions at the individual nodes and the tcl lindex command to obtain the values from these lists. 

# invoke command to determine nodal reactions                                                                                 
reactions

set node1Rxn [nodeReaction 1]; # nodeReaction command returns nodal reactions for specified node in a list  
set node2Rxn [nodeReaction 2]
set node3Rxn [nodeReaction 3]
set node4Rxn [nodeReaction 4]

set inputedFy  [expr -$Load1-$Load2-$Load3]; # loads added negative Fy direction to ele            
set computedFx [expr [lindex $node1Rxn 0]+[lindex $node2Rxn 0]+[lindex $node3Rxn 0]+[lindex $node4Rxn 0]]
set computedFy [expr [lindex $node1Rxn 1]+[lindex $node2Rxn 1]+[lindex $node3Rxn 1]+[lindex $node4Rxn 1]]

puts "\nEqilibrium Check After Gravity:"
puts "SumX: Inputed: 0.0 + Computed: $computedFx = [expr 0.0+$computedFx]"
puts "SumY: Inputed: $inputedFy + Computed: $computedFy = [expr $inputedFy+$computedFy]"


Add Lateral Loads

Now we prepare to add our lateral loads to the model. First we need to set the gravity loads acting constant, i.e. we do not want them changing as we apply more loads to the model. Then we will create load pattern with nodal loads to add to the model. 

# set gravity loads constant and time in domain to 0.0                                           
loadConst -time 0.0

timeSeries Linear 2
pattern Plain 2 2 {
    load 13 220.0 0.0 0.0
    load  9 180.0 0.0 0.0
    load  5  90.0 0.0 0.0
}


Recorder

We will create an element recorder to record the forces at the bottom story columns. 

recorder Element -file eleForces.out -ele 1 4 7 10 forces


Perform The Lateral Load Analysis

After the objects for the model, analysis and output has been defined we now perform the analysis. 

analyze 1


Print Info to Screen to Allow User to Check Results

In addition to using recorders, it is possible to specify output using the print and puts commands. When no file identifiers are provided, these commands will print results to the screen. 

reactions

set node1Rxn [nodeReaction 1]; # nodeReaction command returns nodal reactions for specified node in a list      
set node2Rxn [nodeReaction 2]
set node3Rxn [nodeReaction 3]
set node4Rxn [nodeReaction 4]

set inputedFx  [expr 220.0+180.0+90.0]
set computedFx [expr [lindex $node1Rxn 0]+[lindex $node2Rxn 0]+[lindex $node3Rxn 0]+[lindex $node4Rxn 0]]
set computedFy [expr [lindex $node1Rxn 1]+[lindex $node2Rxn 1]+[lindex $node3Rxn 1]+[lindex $node4Rxn 1]]

puts "\nEqilibrium Check After Lateral Loads:"
puts "SumX: Inputed: $inputedFx + Computed: $computedFx = [expr $inputedFx+$computedFx]"
puts "SumY: Inputed: $inputedFy + Computed: $computedFy = [expr $inputedFy+$computedFy]"

# print ele information for columns at bottom
print ele 1 4 7 19


Finally look at the eigenvalues

After the lateral load analysis has completed we will look at the period of the structure. To do this we use the eigenvalue command to obtain the eigenvalues. These are returned in a tcl list. From the list we obtain the eigenvalue for the mode using the tcl lindex command and use the expr command to determine the period. 

set eigenValues [eigen 5]

puts "\nEigenvalues:"
set eigenValue [lindex $eigenValues 0]
puts "T[expr 0+1] = [expr 2*$PI/sqrt($eigenValue)]"
set eigenValue [lindex $eigenValues 1]
puts "T[expr 1+1] = [expr 2*$PI/sqrt($eigenValue)]"
set eigenValue [lindex $eigenValues 2]
puts "T[expr 2+1] = [expr 2*$PI/sqrt($eigenValue)]"
set eigenValue [lindex $eigenValues 3]
puts "T[expr 3+1] = [expr 2*$PI/sqrt($eigenValue)]"
set eigenValue [lindex $eigenValues 4]
puts "T[expr 4+1] = [expr 2*$PI/sqrt($eigenValue)]"

# create a recorder to record eigenvalues at all free nodes
recorder Node -file eigenvector.out -nodeRange 5 16 -dof 1 2 3 eigen 0

# record the results into the file
record


Results

When you run this script, you should see the following printed to the screen:

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=Elastic_Frame_Example&oldid=8558"