File:Dynamic Analysis of 2-Story Moment Frame.doc: Difference between revisions

From OpenSeesWiki
Jump to navigation Jump to search
mNo edit summary
 
(5 intermediate revisions by the same user not shown)
Line 6: Line 6:


The files needed to analyze this structure in OpenSees are included here:
The files needed to analyze this structure in OpenSees are included here:
* The main file:  [[pushover_concentrated.tcl|dynamic_concentrated.tcl]]
* The main file:  [[MRF_2Story_Concentrated.tcl|MRF_2Story_Concentrated.tcl]]
Supporting procedure files
Supporting procedure files
* [[DisplayModel2D.tcl|DisplayModel2D.tcl]]  – displays a 2D perspective of the model
* [[DisplayModel2D.tcl|DisplayModel2D.tcl]]  – displays a 2D perspective of the model
Line 12: Line 12:
* [[rotSpring2DModIKModel.tcl|rotSpring2DModIKModel.tcl]] – creates a bilinear rotational spring that follows the Modified Ibarra Krawinkler Deterioration Model (used in the concentrated model)
* [[rotSpring2DModIKModel.tcl|rotSpring2DModIKModel.tcl]] – creates a bilinear rotational spring that follows the Modified Ibarra Krawinkler Deterioration Model (used in the concentrated model)
* [[rotLeaningCol.tcl|rotLeaningCol.tcl]] – creates a low-stiffness rotational spring used in a leaning column
* [[rotLeaningCol.tcl|rotLeaningCol.tcl]] – creates a low-stiffness rotational spring used in a leaning column
All files are available in a compressed format here:  [[Media:pushover_example.zip|dynamic_example.zip]]
The acceleration history for the Canoga Park Record (included in the zip file below).
 
All files are available in a compressed format here:  [[Media:dynamic_example.zip|dynamic_example.zip]]


The rest of this example describes the model and shows the analysis results.   
The rest of this example describes the model and shows the analysis results.   
Line 42: Line 44:
For the [[Element Recorder|element recorder]], the [[Region Command|region command]] was used to assign all column springs to one group and all beam springs to a separate group.
For the [[Element Recorder|element recorder]], the [[Region Command|region command]] was used to assign all column springs to one group and all beam springs to a separate group.
It is important to note that the recorders only record information for [[Analyze Command|analyze commands]] that are called after the [[Recorder Command|recorder commands]] are called.  In this example, the recorders are placed after the gravity analysis so that the steps of the gravity analysis do not appear in the output files.
It is important to note that the recorders only record information for [[Analyze Command|analyze commands]] that are called after the [[Recorder Command|recorder commands]] are called.  In this example, the recorders are placed after the gravity analysis so that the steps of the gravity analysis do not appear in the output files.
=== Analysis ===
=== Analysis ===
The structure is first analyzed under gravity loads before the dynamic analysis is conducted.  The gravity loads are applied using a [[Load Control|load-controlled]] static analysis with 10 steps.  After this analysis is completed, the time is reset to zero so that the dynamic analysis starts from time zero.  This is accomplished with the [[LoadConst Command|loadConst command]].
The structure is first analyzed under gravity loads before the dynamic analysis is conducted.  The gravity loads are applied using a [[Load Control|load-controlled]] static analysis with 10 steps.  After this analysis is completed, the time is reset to zero so that the dynamic analysis starts from time zero.  This is accomplished with the [[LoadConst Command|loadConst command]].
For the dynamic analysis, the structure is subjected to the Canoga Park record from the 1994 Northridge earthquake.  To apply the ground motion to the structure, the [[Uniform Exciatation Pattern|uniform excitation pattern]] is used.  The name of the file containing the acceleration record, timestep of the ground motion, scale factor applied to the ground motion, and the direction in which the motion is to be applied must all be specified as part of the [[Uniform Exciatation Pattern|uniform excitation pattern command]].
For the dynamic analysis, the structure is subjected to the Canoga Park record from the 1994 Northridge earthquake.  To apply the ground motion to the structure, the [[Uniform Exciatation Pattern|uniform excitation pattern]] is used.  The name of the file containing the acceleration record, timestep of the ground motion, scale factor applied to the ground motion, and the direction in which the motion is to be applied must all be specified as part of the [[Uniform Exciatation Pattern|uniform excitation pattern command]].
To execute the dynamic analysis, the [[Analyze Command|analyze command]] is used with the specified number of analysis steps and the timestep of the analysis.  The timestep used in the analysis should be less than or equal to the timestep of the input ground motion.
To execute the dynamic analysis, the [[Analyze Command|analyze command]] is used with the specified number of analysis steps and the timestep of the analysis.  The timestep used in the analysis should be less than or equal to the timestep of the input ground motion.
=== Loading ===
Gravity loads are assigned to the beam-column joint nodes using the [[NodalLoad Command|nodal load command]].  Gravity loads tributary to the frame members are assigned to the frame nodes while the remaining gravity loads are applied to the leaning columns.  The gravity loads are applied as a [[Plain Pattern|plain load pattern]] with a [[Constant TimeSeries|constant time series]] since the gravity loads always act on the structure.
In this example, lateral loads are distributed to the frame using the methodology of ASCE 7-10 (http://www.asce.org/Product.aspx?id=2147487569).  Lateral loads are applied to all the frame nodes in a given floor.  A [[Plain Pattern|plain load pattern]] with a [[Linear TimeSeries|linear time series]] is used for lateral load application so that loads increase with time.
=== Recorders ===
The [[Recorder Command|recorders]] used in this example include:
* The [[Drift Recorder|drift recorder]] to track the story and roof drift histories
* The [[Node Recorder|node recorder]] to track the shear force reaction histories at the supports
* The [[Element Recorder|element recorder]] to track the moment and rotation histories of the springs in the concentrated plasticity model
For the [[Element Recorder|element recorder]], the [[Region Command|region command]] was used to assign all column springs to one group and all beam springs to a separate group.
It is important to note that the recorders only record information for [[Analyze Command|analyze commands]] that are called after the [[Recorder Command|recorder commands]] are called.  In this example, the recorders are placed after the gravity analysis so that the steps of the gravity analysis do not appear in the output files.
=== Analysis ===
The structure is first analyzed under gravity loads before the dynamic analysis is conducted.  The gravity loads are applied using a [[Load Control|load-controlled]] static analysis with 10 steps.  After this analysis is completed, the time is reset to zero so that the dynamic analysis starts from time zero.  This is accomplished with the [[LoadConst Command|loadConst command]].
The dynamic analysis is performed using a [[Displacement Control|displacement-controlled]] static analysis.  In this example, the structure was pushed to 10% roof drift, or 32.4”.  The roof node at Pier 1, node 13 in Figures 1 and 2, was chosen as the control node where the displacement was monitored.  Incremental displacement steps of 0.01” were used.  This step size was used because it is small enough to capture the progression of hinge formation and generate a smooth backbone curve, but not too small that it makes the analysis time unreasonable.


== Results ==
== Results ==


[[File:pushover_curve.png|frame|Figure 3.  Pushover Curve]]
[[File:Dhist_plot_ConcDynam.png|frame|Figure 2.  Floor Displacement History]]


The results of the pushover analysis are shown in Figure 3.  This figure shows the normalized base shear (weight of the structure divided by the base shear) versus the roof drift (roof displacement divided by the roof elevation).  The models are nearly identical until about 2.5% roof drift when their curves begin to diverge.  The descending branch of the the concentrated plasticity model is slightly steeper, but the two models agree reasonably well as there is less than 10% percent difference in the base shears at 10% roof drift.  
The floor displacement results of the dynamic analysis are shown in Figure 2.  The top graph shows the ground acceleration history while the middle and bottom graphs show the displacement time histories of the 3rd floor (roof) and 2nd floor, respectively.


== References ==
== References ==

Latest revision as of 16:22, 2 September 2010

Example posted by: Laura Eads, Stanford University

This example demonstrates how to perform a dynamic analysis in OpenSees using a 2-story, 1-bay steel moment resisting frame. The structure is subjected to the Canoga Park record from the 1994 Northridge earthquake. The nonlinear behavior is represented using the concentrated plasticity concept with rotational springs. The rotational behavior of the plastic regions in both models follows a bilinear hysteretic response based on the Modified Ibarra Krawinkler Deterioration Model (Ibarra et al. 2005, Lignos and Krawinkler 2009, 2010). For this example, all modes of cyclic deterioration are neglected. A leaning column carrying gravity loads is linked to the frame to simulate P-Delta effects.

The files needed to analyze this structure in OpenSees are included here:

Supporting procedure files

The acceleration history for the Canoga Park Record (included in the zip file below).

All files are available in a compressed format here: dynamic_example.zip

The rest of this example describes the model and shows the analysis results.

Model Description

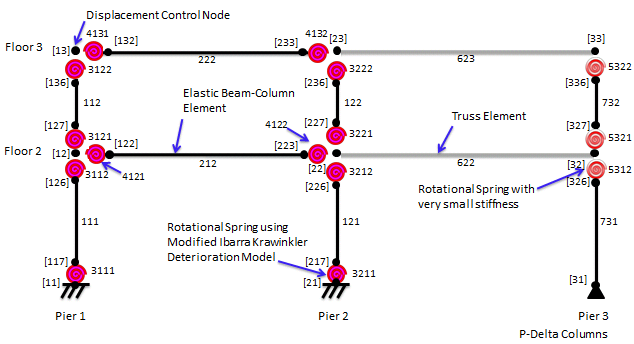
Figure 1. Schematic representation of concentrated plasticity OpenSees model with element number labels and [node number] labels. Note: The springs are zeroLength elements, but their sizes are greatly exaggerated in this figure for clarity.

The 2-story, 1-bay steel moment resisting frame is modeled with elastic beam-column elements connected by zeroLength elements which serve as rotational springs to represent the structure’s nonlinear behavior. The springs follow a bilinear hysteretic response based on the Modified Ibarra Krawinkler Deterioration Model. A leaning column with gravity loads is linked to the frame by truss elements to simulate P-Delta effects. An idealized schematic of the model is presented in Figure 1. A leaning column with gravity loads is linked to the frame by truss elements to simulate P-Delta effects. To simplify this model, panel zone contributions are neglected and plastic hinges form at the beam-column joints, i.e., centerline dimensions are used. Subsequent examples will explicitly model the panel zone shear distortions and include reduced beam sections (RBS). The units of the model are kips, inches, and seconds. For a detailed description of this model, see Pushover Analysis of 2-Story Moment Frame.

Damping and the Rayleigh Command

This model uses Rayleigh damping which formulates the damping matrix as a linear combination of the mass matrix and stiffness matrix: c = a0*m + a1*k, where a0 is the mass proportional damping coefficient and a1 is the stiffness proportional damping coefficient. A damping ratio of two percent, which is a typical value for steel buildings, is assigned to the first two modes of the structure. The rayleigh command allows the user to specify whether the initial, current, or last committed stiffness matrix is used in the damping formulation. In this example, only the initial stiffness matrix is used by assigning values of 0.0 to the other stiffness matrix coefficients. To properly model the structure, stiffness proportional damping is applied only to the frame elements and not to the highly rigid truss elements that link the frame and P-Delta columns, nor to the P-Delta columns themselves. OpenSees does not apply stiffness proportional damping to zeroLength elements. In order to apply damping to only certain elements, the rayleigh command is used in combination with the region command. As noted in the region command documentation, the region cannot be defined by BOTH elements and nodes. Because mass proportional damping assigns damping to nodes with mass, OpenSees will ignore any mass proportional damping that is assigned using the rayleigh command in combination with the region command for a region of elements. Therefore, if using the region command to assign damping, the mass proportional damping and stiffness proportional damping must be assigned in separate steps.

Modifications to the Stiffness Proportional Damping Coefficient

As described in the “Stiffness Modifications to Elastic Frame Elements” section of Pushover Analysis of 2-Story Moment Frame, the stiffness of the elastic frame elements has been modified. As explained in Ibarra and Krawinkler (2005) and Zareian and Medina (2010), the stiffness proportional damping coefficient that is used with these elements must also be modified. As the stiffness of the elastic elements was made “(n+1)/n” times greater than the stiffness of the actual frame member, the stiffness proportional damping coefficient of these elements must also be made “(n+1)/n” times greater than the traditional stiffness proportional damping coefficient.

Dynamic Analysis

Recorders

The recorders used in this example include:

  • The drift recorder to track the story and roof drift histories
  • The node recorder to track the shear force reaction histories at the supports
  • The element recorder to track the moment and rotation histories of the springs in the concentrated plasticity model

For the element recorder, the region command was used to assign all column springs to one group and all beam springs to a separate group. It is important to note that the recorders only record information for analyze commands that are called after the recorder commands are called. In this example, the recorders are placed after the gravity analysis so that the steps of the gravity analysis do not appear in the output files.

Analysis

The structure is first analyzed under gravity loads before the dynamic analysis is conducted. The gravity loads are applied using a load-controlled static analysis with 10 steps. After this analysis is completed, the time is reset to zero so that the dynamic analysis starts from time zero. This is accomplished with the loadConst command. For the dynamic analysis, the structure is subjected to the Canoga Park record from the 1994 Northridge earthquake. To apply the ground motion to the structure, the uniform excitation pattern is used. The name of the file containing the acceleration record, timestep of the ground motion, scale factor applied to the ground motion, and the direction in which the motion is to be applied must all be specified as part of the uniform excitation pattern command. To execute the dynamic analysis, the analyze command is used with the specified number of analysis steps and the timestep of the analysis. The timestep used in the analysis should be less than or equal to the timestep of the input ground motion.

Results

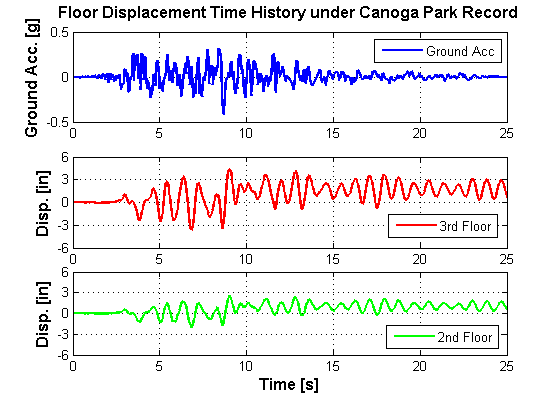
Figure 2. Floor Displacement History

The floor displacement results of the dynamic analysis are shown in Figure 2. The top graph shows the ground acceleration history while the middle and bottom graphs show the displacement time histories of the 3rd floor (roof) and 2nd floor, respectively.

References

  1. Ibarra, L. F., and Krawinkler, H. (2005). “Global collapse of frame structures under seismic excitations,” Technical Report 152, The John A. Blume Earthquake Engineering Research Center, Department of Civil Engineering, Stanford University, Stanford, CA. [electronic version: http://blume.stanford.edu/Blume/TRList.htm]
  2. Ibarra, L. F., Medina, R. A., and Krawinkler, H. (2005). “Hysteretic models that incorporate strength and stiffness deterioration,” Earthquake Engineering and Structural Dynamics, Vol. 34, 12, pp. 1489-1511.
  3. Lignos, D. G., and Krawinkler, H. (2009). “Sidesway Collapse of Deteriorating Structural Systems under Seismic Excitations,” Technical Report 172, The John A. Blume Earthquake Engineering Research Center, Department of Civil Engineering, Stanford University, Stanford, CA.
  4. Lignos, D. G., and Krawinkler, H. (2010). “Deterioration Modeling of Steel Beams and Columns in Support to Collapse Prediction of Steel Moment Frames,” ASCE, Journal of Structural Engineering (under review).
  5. Zareian, F. and Medina, R. A. (2010). “A practical method for proper modeling of structural damping in inelastic plane structural systems,” Computers & Structures, Vol. 88, 1-2, pp. 45-53.

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeDimensionsUserComment
current07:54, 2 September 2010 (40 KB)Leads (talk | contribs)

You cannot overwrite this file.

There are no pages that use this file.

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=File:Dynamic_Analysis_of_2-Story_Moment_Frame.doc&oldid=5071"