SAWS Material: Difference between revisions

From OpenSeesWiki
Jump to navigation Jump to search
(Imported PYSimple1 to start)
 
No edit summary
 
(6 intermediate revisions by one other user not shown)
Line 1: Line 1:
This command is used to construct a uniaxial Kent-Scott-Park concrete material object with degraded linear unloading/reloading stiffness according to the work of Karsan-Jirsa and no tensile strength. (REF: Fedeas).
{{CommandManualMenu}}
 
This file contains the class definition for  SAWSMaterial.  SAWSMaterial provides the implementation of a one-dimensional hysteretic model develeped as part of the CUREe Caltech wood frame project.  




{|  
{|  
| style="background:yellow; color:black; width:800px" | '''uniaxialMaterial PySimple1 $matTag $soilType $pult $Y50 $Cd <$c>'''
| style="background:yellow; color:black; width:800px" | '''uniaxialMaterial SAWS $tag $F0 $FI $DU $S0 $R1 $R2 $R3 $R4 $alph $beta'''
|}
|}


Line 11: Line 13:
|  style="width:150px" | '''$matTag ''' || integer tag identifying material
|  style="width:150px" | '''$matTag ''' || integer tag identifying material
|-
|-
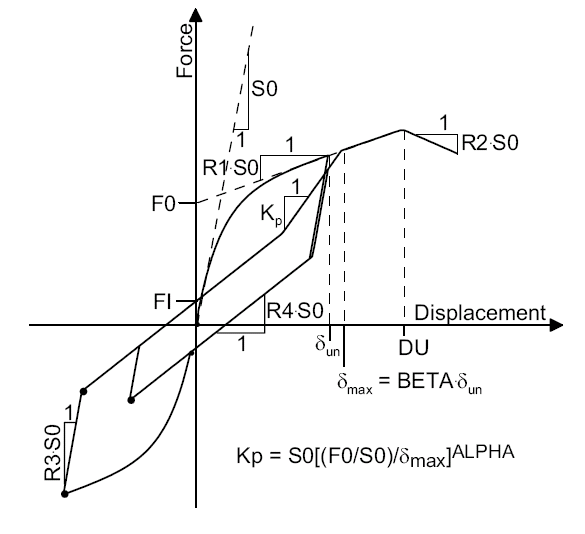
|  '''$soilType ''' || soilType = 1 Backbone of p-y curve approximates Matlock (1970) soft clay relation.
|  '''$F0 ''' || Intercept strength of the shear wall spring element for the asymtotic line to the envelope curve F0 > FI > 0
 
|-
soilType = 2 Backbone of p-y curve approximates API (1993) sand relation.
|  '''$FI ''' || Intercept strength of the spring element for the pinching branch of the hysteretic
curve. (FI > 0).
|-
|  '''$DU ''' || Spring element displacement at ultimate load. (DU > 0).
|-
|  '''$S0 ''' || Initial stiffness of the shear wall spring element (S0 > 0).
|-
| '''$R1''' || Stiffness ratio of the asymptotic line to the spring element envelope curve. The
slope of this line is R1 S0. (0 < R1 < 1.0).
|-
| '''$R2''' || Stiffness ratio of the descending branch of the spring element envelope curve. The
slope of this line is R2 S0. ( R2 < 0).
|-
|-
| '''$pult ''' || Ultimate capacity of the p-y material. Note that "p" or "pult" are distributed loads [force per length of pile] in common design equations, but are both loads for this uniaxialMaterial [i.e., distributed load times the tributary length of the pile].
| '''$R3''' || Stiffness ratio of the unloading branch off the spring element envelope curve. The
slope of this line is R3 S0. ( R3  1).
|-
|-
| '''$Y50 ''' || Displacement at which 50% of pult is mobilized in monotonic loading.
| '''$R4''' || Stiffness ratio of the pinching branch for the spring element. The slope of this line
is R4 S0. ( R4 > 0).
|-
|-
| '''$Cd ''' || Variable that sets the drag resistance within a fully-mobilized gap as Cd*pult.
| '''$alpha''' || Stiffness degradation parameter for the shear wall spring element. (ALPHA > 0).
|-
|-
| '''$c''' || The viscous damping term (dashpot) on the far-field (elastic) component of the displacement rate (velocity). (optional Default = 0.0). Nonzero c values are used to represent radiation damping effects
| '''$beta''' || Stiffness degradation parameter for the spring element. (BETA > 0).
|}
|}


NOTES:


In general the HHT algorithm is preferred over a Newmark algorithm when using this material. This is due to the numerical oscillations that can develop with viscous damping forces under transient loading with certain solution algorithms and damping ratios.
== Notes: ==
 
Refer to the figure below for more information, and the reference provided at the end of this page for complete details about modeling assumptions.
 
 
[[File:FolzFigure.gif]]
 
 
 
== Example Files: ==


''Click to download files''


[[Image:PySimple1A.gif]]
[[Media:Test.tcl]]


[[Media:SAWSZeroLength.tcl]]


[[Image:PySimple1B.gif]]
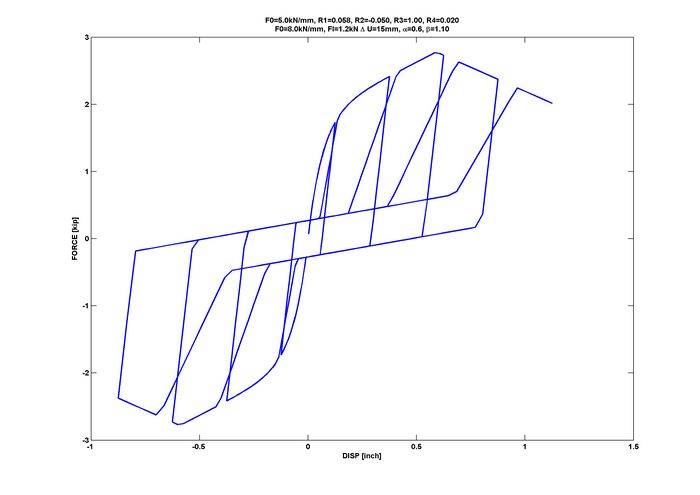
== Example: Hysteresis ==
[[File:TestHysteresis.jpg|700px]]


EXAMPLE:








REFERENCES:
== References ==


"Seismic Soil-pile-strcture interaction experiments and analysis", Boulanger, R.w., Curras, C.J., Kutter, B.L., Wilson, D.W., and Abghari, A. (1990). Jornal of Geotechnical and Geoenvironmental Engineering, ASCS, 125(9):750-759.
Reference: Folz, B. and Filiatrault, A. (2001). "SAWS - Version 1.0, A Computer Program for the Seismic Analysis of Woodframe Structures", Structural Systems Research Project Report No. SSRP-2001/09, Dept. of Structural Engineering, UCSD, La Jolla, CA .


----
----


Code Developed by: <span style="color:blue"> Ross Boulanger, UC Davis </span>
Code Developed by: <span style="color:blue"> Patxi Uriz, Exponent </span> (Converted from FORTRAN code originally written by Bryan Folz)

Latest revision as of 21:13, 3 March 2010



This file contains the class definition for SAWSMaterial. SAWSMaterial provides the implementation of a one-dimensional hysteretic model develeped as part of the CUREe Caltech wood frame project.


uniaxialMaterial SAWS $tag $F0 $FI $DU $S0 $R1 $R2 $R3 $R4 $alph $beta
$matTag integer tag identifying material
$F0 Intercept strength of the shear wall spring element for the asymtotic line to the envelope curve F0 > FI > 0
$FI Intercept strength of the spring element for the pinching branch of the hysteretic

curve. (FI > 0).

$DU Spring element displacement at ultimate load. (DU > 0).
$S0 Initial stiffness of the shear wall spring element (S0 > 0).
$R1 Stiffness ratio of the asymptotic line to the spring element envelope curve. The

slope of this line is R1 S0. (0 < R1 < 1.0).

$R2 Stiffness ratio of the descending branch of the spring element envelope curve. The

slope of this line is R2 S0. ( R2 < 0).

$R3 Stiffness ratio of the unloading branch off the spring element envelope curve. The

slope of this line is R3 S0. ( R3 1).

$R4 Stiffness ratio of the pinching branch for the spring element. The slope of this line

is R4 S0. ( R4 > 0).

$alpha Stiffness degradation parameter for the shear wall spring element. (ALPHA > 0).
$beta Stiffness degradation parameter for the spring element. (BETA > 0).


Notes:

Refer to the figure below for more information, and the reference provided at the end of this page for complete details about modeling assumptions.



Example Files:

Click to download files

Media:Test.tcl

Media:SAWSZeroLength.tcl

Example: Hysteresis



References

Reference: Folz, B. and Filiatrault, A. (2001). "SAWS - Version 1.0, A Computer Program for the Seismic Analysis of Woodframe Structures", Structural Systems Research Project Report No. SSRP-2001/09, Dept. of Structural Engineering, UCSD, La Jolla, CA .

Code Developed by: Patxi Uriz, Exponent (Converted from FORTRAN code originally written by Bryan Folz)

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=SAWS_Material&oldid=2745"