ViscousDamper Material: Difference between revisions

From OpenSeesWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(One intermediate revision by the same user not shown)
Line 63: Line 63:
|  style="width:5px" | '''[1]''' || Akcelyan, S., Lignos, D. G., Hikino, T., and Nakashima, M. (2016). “Evaluation of simplified and state-of-the-art analysis procedures for steel frame buildings equipped with supplemental damping devices based on E-Defense full-scale shake table tests.” Journal of Structural Engineering, 142(6), 04016024. [http://ascelibrary.org/doi/ref/10.1061/%28ASCE%29ST.1943-541X.0001474]
|  style="width:5px" | '''[1]''' || Akcelyan, S., Lignos, D. G., Hikino, T., and Nakashima, M. (2016). “Evaluation of simplified and state-of-the-art analysis procedures for steel frame buildings equipped with supplemental damping devices based on E-Defense full-scale shake table tests.” Journal of Structural Engineering, 142(6), 04016024. [http://ascelibrary.org/doi/ref/10.1061/%28ASCE%29ST.1943-541X.0001474]
|-
|-
|  style="width:5px" | '''[2]''' || Akcelyan, S., Lignos, D. G., Hikino, T. (2018). “Adaptive Numerical Method Algorithms for Nonlinear Viscous and Bilinear Oil Damper Models Subjected to Dynamic Loading.” Soil Dynamics and Earthquake Engineering, XXX(X), XXXXXXX. [http://www.journals.elsevier.com/soil-dynamics-and-earthquake-engineering].
|  style="width:5px" | '''[2]''' || Akcelyan, S., Lignos, D. G., Hikino, T. (2018). “Adaptive Numerical Method Algorithms for Nonlinear Viscous and Bilinear Oil Damper Models Subjected to Dynamic Loading.” Soil Dynamics and Earthquake Engineering, 113, 488-502. [http://doi.org/10.1016/j.soildyn.2018.06.021].
|-
|-
|  style="width:5px" | '''[3]''' || Akcelyan, S. (2017). "Seismic retrofit of existing steel tall buildings with supplemental damping devices."  Ph.D. Dissertation, McGill University, Canada.
|  style="width:5px" | '''[3]''' || Akcelyan, S. (2017). "Seismic retrofit of existing steel tall buildings with supplemental damping devices."  Ph.D. Dissertation, McGill University, Canada.
Line 72: Line 72:
|-
|-
|}
|}
Code Developed and Implemented by : <span style="color:blue">  '''''[http://www.researchgate.net/profile/Sarven_Akcelyan2 Sarven Akcelyan]''''' & '''''[http://dimitrios-lignos.research.mcgill.ca/PLignos.html Prof. Dimitrios G. Lignos]''''', (McGill University) </span>
Code Developed and Implemented by : <span style="color:blue">  '''''[http://sarvenakcelyan.com Sarven Akcelyan]''''' & '''''[http://dimitrios-lignos.research.mcgill.ca/PLignos.html Prof. Dimitrios G. Lignos]''''', (McGill University) </span>

Latest revision as of 17:23, 19 July 2018



This command is used to construct a ViscousDamper material, which represents the Maxwell Model (linear spring and nonlinear dashpot in series). The ViscousDamper material simulates the hysteretic response of nonlinear viscous dampers. An adaptive iterative algorithm has been implemented and validated to solve numerically the constitutive equations within a nonlinear viscous damper with a high-precision accuracy.

uniaxialMaterial ViscousDamper $matTag $K $Cd $alpha <$LGap> < $NM $RelTol $AbsTol $MaxHalf>
$matTag integer tag identifying material
$K Elastic stiffness of linear spring to model the axial flexibility of a viscous damper (e.g. combined stiffness of the supporting brace and internal damper portion)
$Cd Damping coefficient
$alpha Velocity exponent
$LGap Gap length to simulate the gap length due to the pin tolerance
$NM Employed adaptive numerical algorithm (default value NM = 1; 1 = Dormand-Prince54, 2=6th order Adams-Bashforth-Moulton, 3=modified Rosenbrock Triple)
$RelTol Tolerance for absolute relative error control of the adaptive iterative algorithm (default value 10^-6)
$AbsTol Tolerance for absolute error control of adaptive iterative algorithm (default value 10^-10)
$MaxHalf Maximum number of sub-step iterations within an integration step (default value 15)

Examples:

1. Input parameters:
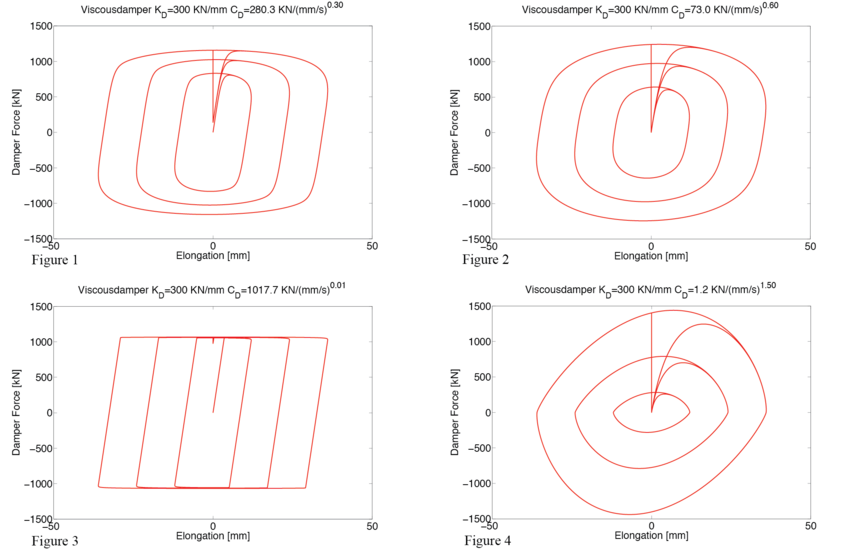
Assume a viscous damper with axial stiffness K=300.0kN/mm, damping coefficient Cd=280.3kN(s/mm)0.3, and exponent a=0.30.
The input parameters for the material should be as follows:
uniaxialMaterial ViscousDamper 1 300 280.3 0.30
Using these properties, Figure 1 shows the hysteretic response of this damper for sinusoidal displacement increments of 12, 24 and 36mm and a frequency f = 0.5Hz.
The sensitivity of the viscous damper with respect to its velocity exponent is shown in Figures 2 to 4 for the following set of parameters:
Viscous Damper with various input parameter variations
2. Single story single bay frame with viscous damper

References:

[1] Akcelyan, S., Lignos, D. G., Hikino, T., and Nakashima, M. (2016). “Evaluation of simplified and state-of-the-art analysis procedures for steel frame buildings equipped with supplemental damping devices based on E-Defense full-scale shake table tests.” Journal of Structural Engineering, 142(6), 04016024. [1]
[2] Akcelyan, S., Lignos, D. G., Hikino, T. (2018). “Adaptive Numerical Method Algorithms for Nonlinear Viscous and Bilinear Oil Damper Models Subjected to Dynamic Loading.” Soil Dynamics and Earthquake Engineering, 113, 488-502. [2].
[3] Akcelyan, S. (2017). "Seismic retrofit of existing steel tall buildings with supplemental damping devices." Ph.D. Dissertation, McGill University, Canada.
[4] Oohara, K., and Kasai, K. (2002), “Time-History Analysis Models for Nonlinear Viscous Dampers”, Proc. Structural Engineers World Congress (SEWC), Yokohama, JAPAN, CD-ROM, T2-2-b-3 (in Japanese).
[5] Kasai K, Oohara K. “Algorithm and Computer Code To Simulate Response of Nonlinear Viscous Damper” Passively Controlled Structure Symposium 2001, Yokohama, Japan (in Japanese).

Code Developed and Implemented by : Sarven Akcelyan & Prof. Dimitrios G. Lignos, (McGill University)

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=ViscousDamper_Material&oldid=12561"