Bilin Material: Difference between revisions

From OpenSeesWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(10 intermediate revisions by 3 users not shown)
Line 1: Line 1:
{{CommandManualMenu}}
{{CommandManualMenu}}


This command is used to construct a bilin material. The bilin material simulates the modified Ibarra-Krawinkler deterioration model with bilinear hysteretic response.
This command is used to construct a bilin material. The bilin material simulates the modified Ibarra-Medina-Krawinkler deterioration model with bilinear hysteretic response. Note that the hysteretic response of this material has been calibrated with respect to more than 350 experimental data of steel beam-to-column connections and multivariate regression formulas are provided to estimate the deterioration parameters of the model for different connection types. These relationships were developed by Lignos and Krawinkler (2009, 2011) and have been adopted by PEER/ATC (2010). [[NOTE: before you use this material make sure that you have downloaded the latest OpenSees version.]]


{|  
{|  
| style="background:yellow; color:black; width:800px" | '''uniaxialMaterial Bilin  $matTag  $K0  $as_Plus  $as_Neg  $My_Plus  $My_Neg  $Lamda_S  $Lamda_C  $Lamda_A  $Lamda_K  $c_S  $c_C  $c_A  $c_K  $theta_p_Plus  $theta_p_Neg  $theta_pc_Plus  $theta_pc_Neg  $Res_Pos  $Res_Neg  $theta_u_Plus  $theta_u_Neg  $D_Plus  $D_Neg'''
| style="background:yellow; color:black; width:800px" | '''uniaxialMaterial Bilin  $matTag  $K0  $as_Plus  $as_Neg  $My_Plus  $My_Neg  $Lamda_S  $Lamda_C  $Lamda_A  $Lamda_K  $c_S  $c_C  $c_A  $c_K  $theta_p_Plus  $theta_p_Neg  $theta_pc_Plus  $theta_pc_Neg  $Res_Pos  $Res_Neg  $theta_u_Plus  $theta_u_Neg  $D_Plus  $D_Neg <$nFactor>'''
|}
|}


Line 20: Line 20:
|  '''$My_Plus ''' || effective yield strength for positive loading direction
|  '''$My_Plus ''' || effective yield strength for positive loading direction
|-
|-
|  '''$My_Neg ''' || effective yield strength for negative loading direction
|  '''$My_Neg ''' || effective yield strength for negative loading direction (negative value)
|-
|-
|  '''$Lamda_S ''' || Cyclic deterioration parameter for strength deterioration
|  '''$Lamda_S ''' || Cyclic deterioration parameter for strength deterioration
Line 30: Line 30:
|  '''$Lamda_K''' || Cyclic deterioration parameter for unloading stiffness deterioration
|  '''$Lamda_K''' || Cyclic deterioration parameter for unloading stiffness deterioration
|-
|-
|  '''$c_S''' || rate of strength deterioration
|  '''$c_S''' || rate of strength deterioration. The default value is 1.0.
|-
|-
|  '''$c_C''' || rate of post-capping strength deterioration
|  '''$c_C''' || rate of post-capping strength deterioration. The default value is 1.0.
|-
|-
|  '''$c_A''' || rate of accelerated reloading deterioration
|  '''$c_A''' || rate of accelerated reloading deterioration. The default value is 1.0.
|-
|-
|  '''$c_K''' || rate of unloading stiffness deterioration
|  '''$c_K''' || rate of unloading stiffness deterioration. The default value is 1.0.
|-
|-
|  '''$theta_p_Plus''' || pre-capping rotation for positive loading direction (often noted as plastic rotation capacity)
|  '''$theta_p_Plus''' || pre-capping rotation for positive loading direction (often noted as plastic rotation capacity)
|-
|-
|  '''$theta_p_Neg''' || pre-capping rotation for negative loading direction (often noted as plastic rotation capacity)
|  '''$theta_p_Neg''' || pre-capping rotation for negative loading direction (often noted as plastic rotation capacity) (positive value)
|-
|-
|  '''$theta_pc_Plus''' || post-capping rotation for positive loading direction
|  '''$theta_pc_Plus''' || post-capping rotation for positive loading direction
|-
|-
|  '''$theta_pc_Neg''' || post-capping rotation for negative loading direction
|  '''$theta_pc_Neg''' || post-capping rotation for negative loading direction (positive value)
|-
|-
|  '''$Res_Pos''' || residual strength ratio for positive loading direction
|  '''$Res_Pos''' || residual strength ratio for positive loading direction
|-
|-
| ''' $Res_Neg''' || residual strength ratio for negative loading direction
| ''' $Res_Neg''' || residual strength ratio for negative loading direction (positive value)
|-
|-
| ''' $theta_u_Plus'''  || ultimate rotation capacity for positive loading direction
| ''' $theta_u_Plus'''  || ultimate rotation capacity for positive loading direction
|-
|-
| '''$theta_u_Neg''' || ultimate rotation capacity for negative loading direction
| '''$theta_u_Neg''' || ultimate rotation capacity for negative loading direction (positive value)
|-
|-
| '''$D_Plus''' || rate of cyclic deterioration in the positive loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam)
| '''$D_Plus''' || rate of cyclic deterioration in the positive loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0.
|-
|-
| '''$D_Neg''' || rate of cyclic deterioration in the negative loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam)
| '''$D_Neg''' || rate of cyclic deterioration in the negative loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0.
|-
| '''$nFactor''' || elastic stiffness amplification factor, mainly for use with concentrated plastic hinge elements (optional, default = 0).
|-
|-
|}
|}
Line 63: Line 65:
[[Image:ModIKModel.PNG]]
[[Image:ModIKModel.PNG]]


'''Image from: Lignos and Krawinkler (2009, 2010a)'''
'''Image from: Lignos et al. (2011)'''


The deterioration model parameters can be calibrated based on actual experimental data of steel components. Instead, a user can determine the same parameters with predictive equations that have been developed by Lignos and Krawinkler (2009, 2011). These equations relate deterioration modelling parameters with geometric and material properties of steel components and have been developed with multivariate regression analysis after extensive calibration of a recently developed steel component database of more than 300 steel specimens (Lignos and Krawinkler 2007, 2009, 2011).
The deterioration model parameters can be calibrated based on actual experimental data of steel components. Instead, a user can determine the same parameters with predictive equations that have been developed by Lignos and Krawinkler (2009, 2011). These equations relate deterioration modelling parameters with geometric and material properties of steel components and have been developed with multivariate regression analysis after extensive calibration of a recently developed steel component database of more than 300 steel specimens (Lignos and Krawinkler 2007, 2009, 2011).
Line 80: Line 82:
| '''[5] ''' || Lignos,  D.G., Krawinkler, H. (2009). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Rep.No.TB 172, The John A. Blume Earthquake Engineering Research Center, Stanford University, Stanford, CA.
| '''[5] ''' || Lignos,  D.G., Krawinkler, H. (2009). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Rep.No.TB 172, The John A. Blume Earthquake Engineering Research Center, Stanford University, Stanford, CA.
|-
|-
|  '''[6] ''' || Lignos, D. G., Krawinkler, H. and Whittaker, A.S. (2010a). "Prediction and validation of sidesway collapse of two scale models of a 4-story steel moment frame", Earthquake Engineering and Structural Dynamics, EESD, (Accepted for publication, June 14th 2010).
|  '''[6] ''' || Lignos, D. G., Krawinkler, H. and Whittaker, A.S. (2011). "Prediction and validation of sidesway collapse of two scale models of a 4-story steel moment frame", Earthquake Engineering and Structural Dynamics, EESD, Vol. 40 (7), 807-825.
|-
|-
|  '''[7] ''' || Lignos, D.G., and Krawinkler, H. (2010b). “A steel database for component deterioration of tubular hollow square steel columns under varying axial load for collapse assessment of steel structures under earthquakes”, Proc. 7th International Conference on Urban Earthquake Engineering (7CUEE), March 3-5, Tokyo, Japan.
|  '''[7] ''' || Lignos, D.G., and Krawinkler, H. (2010b). “A steel database for component deterioration of tubular hollow square steel columns under varying axial load for collapse assessment of steel structures under earthquakes”, Proc. 7th International Conference on Urban Earthquake Engineering (7CUEE), March 3-5, Tokyo, Japan.
|-
|-
|  '''[8] ''' || Lignos, D.G., and Krawinkler, H. (2011). “Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading”, Journal of Structural Engineering, ASCE (accepted for publication).
|  '''[8] ''' || Lignos, D.G., and Krawinkler, H. (2011). “Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading”, Journal of Structural Engineering, ASCE, Vol. 137 (11), 1291-1302. [[File:BilinMaterialOpenSees.pdf]]
|-
|'''[9] ''' || PEER/ATC (2010). “Modeling and acceptance criteria for seismic design and analysis of tall buildings”, PEER/ATC-72-1, prepared by the Applied Technology Council in cooperation with the Pacific Earthquake Engineering Research Center, Redwood City, CA..
|-
|-
|}
|}
Code Developed by : <span style="color:blue"> by Dr. Dimitrios G. Lignos, McGill University and was implemented by Dr. Theodore Karavasilis, Oxford University </span>
Code Developed by : <span style="color:blue"> by Dr. Dimitrios G. Lignos, McGill University and was implemented by Dr. Theodore Karavasilis, Oxford University </span>
nFactor Implemented by: <span style="color:blue"> by Dr. Andre R. Barbosa, Oregon State University and Mr. Filipe L.A. Ribeiro, Universidade Nova de Lisboa </span>

Latest revision as of 14:59, 3 July 2013



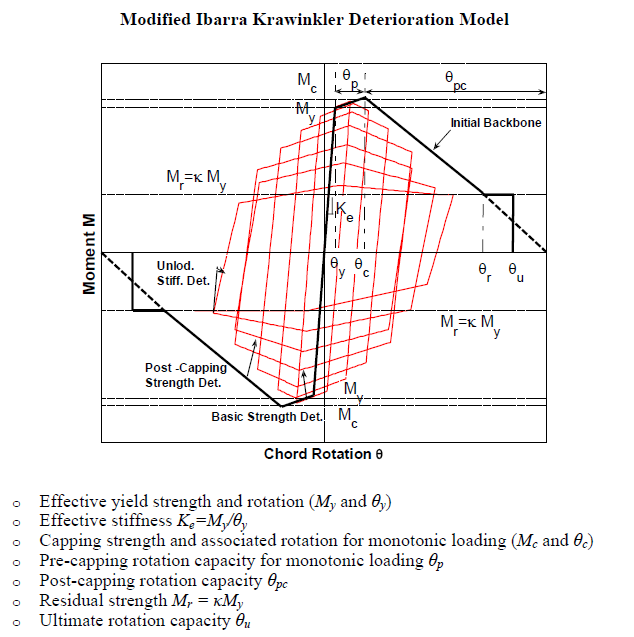
This command is used to construct a bilin material. The bilin material simulates the modified Ibarra-Medina-Krawinkler deterioration model with bilinear hysteretic response. Note that the hysteretic response of this material has been calibrated with respect to more than 350 experimental data of steel beam-to-column connections and multivariate regression formulas are provided to estimate the deterioration parameters of the model for different connection types. These relationships were developed by Lignos and Krawinkler (2009, 2011) and have been adopted by PEER/ATC (2010). NOTE: before you use this material make sure that you have downloaded the latest OpenSees version.

uniaxialMaterial Bilin $matTag $K0 $as_Plus $as_Neg $My_Plus $My_Neg $Lamda_S $Lamda_C $Lamda_A $Lamda_K $c_S $c_C $c_A $c_K $theta_p_Plus $theta_p_Neg $theta_pc_Plus $theta_pc_Neg $Res_Pos $Res_Neg $theta_u_Plus $theta_u_Neg $D_Plus $D_Neg <$nFactor>
$matTag integer tag identifying material
$K0 elastic stiffness
$as_Plus strain hardening ratio for positive loading direction
$as_Neg strain hardening ratio for negative loading direction
$My_Plus effective yield strength for positive loading direction
$My_Neg effective yield strength for negative loading direction (negative value)
$Lamda_S Cyclic deterioration parameter for strength deterioration
$Lamda_C Cyclic deterioration parameter for post-capping strength deterioration
$Lamda_A Cyclic deterioration parameter for acceleration reloading stiffness deterioration (is not a deterioration mode for a component with Bilinear hysteretic response).
$Lamda_K Cyclic deterioration parameter for unloading stiffness deterioration
$c_S rate of strength deterioration. The default value is 1.0.
$c_C rate of post-capping strength deterioration. The default value is 1.0.
$c_A rate of accelerated reloading deterioration. The default value is 1.0.
$c_K rate of unloading stiffness deterioration. The default value is 1.0.
$theta_p_Plus pre-capping rotation for positive loading direction (often noted as plastic rotation capacity)
$theta_p_Neg pre-capping rotation for negative loading direction (often noted as plastic rotation capacity) (positive value)
$theta_pc_Plus post-capping rotation for positive loading direction
$theta_pc_Neg post-capping rotation for negative loading direction (positive value)
$Res_Pos residual strength ratio for positive loading direction
$Res_Neg residual strength ratio for negative loading direction (positive value)
$theta_u_Plus ultimate rotation capacity for positive loading direction
$theta_u_Neg ultimate rotation capacity for negative loading direction (positive value)
$D_Plus rate of cyclic deterioration in the positive loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0.
$D_Neg rate of cyclic deterioration in the negative loading direction (this parameter is used to create assymetric hysteretic behavior for the case of a composite beam). For symmetric hysteretic response use 1.0.
$nFactor elastic stiffness amplification factor, mainly for use with concentrated plastic hinge elements (optional, default = 0).


Image from: Lignos et al. (2011)

The deterioration model parameters can be calibrated based on actual experimental data of steel components. Instead, a user can determine the same parameters with predictive equations that have been developed by Lignos and Krawinkler (2009, 2011). These equations relate deterioration modelling parameters with geometric and material properties of steel components and have been developed with multivariate regression analysis after extensive calibration of a recently developed steel component database of more than 300 steel specimens (Lignos and Krawinkler 2007, 2009, 2011).

References:

[1] Ibarra L.F., and Krawinkler, H. (2005). “Global collapse of frame structures under seismic excitations”, Rep. No. TB 152, The John A. Blume Earthquake Engineering Center, Stanford University, Stanford, CA.
[2] Ibarra L.F., Medina R. A., and Krawinkler H. (2005). “Hysteretic models that incorporate strength and stiffness deterioration”, Earthquake Engineering and Structural Dynamics, 34(12), 1489-1511.
[3] Karavasilis T.L., Ricles J.M., Sause R. (2009). "Implementation of deterioration elements in OpenSEES for collapse simulations" ATLSS Engineering Research Center, Rep. No. 09-11.
[4] Lignos, D.G., and Krawinkler, H. (2007), “A database in support of modeling of component deterioration for collapse prediction of steel frame structures”, Proc. ASCE Structures Congress, Long Beach CA, SEI institute.
[5] Lignos, D.G., Krawinkler, H. (2009). “Sidesway collapse of deteriorating structural systems under seismic excitations,” Rep.No.TB 172, The John A. Blume Earthquake Engineering Research Center, Stanford University, Stanford, CA.
[6] Lignos, D. G., Krawinkler, H. and Whittaker, A.S. (2011). "Prediction and validation of sidesway collapse of two scale models of a 4-story steel moment frame", Earthquake Engineering and Structural Dynamics, EESD, Vol. 40 (7), 807-825.
[7] Lignos, D.G., and Krawinkler, H. (2010b). “A steel database for component deterioration of tubular hollow square steel columns under varying axial load for collapse assessment of steel structures under earthquakes”, Proc. 7th International Conference on Urban Earthquake Engineering (7CUEE), March 3-5, Tokyo, Japan.
[8] Lignos, D.G., and Krawinkler, H. (2011). “Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading”, Journal of Structural Engineering, ASCE, Vol. 137 (11), 1291-1302. File:BilinMaterialOpenSees.pdf
[9] PEER/ATC (2010). “Modeling and acceptance criteria for seismic design and analysis of tall buildings”, PEER/ATC-72-1, prepared by the Applied Technology Council in cooperation with the Pacific Earthquake Engineering Research Center, Redwood City, CA..

Code Developed by : by Dr. Dimitrios G. Lignos, McGill University and was implemented by Dr. Theodore Karavasilis, Oxford University

nFactor Implemented by: by Dr. Andre R. Barbosa, Oregon State University and Mr. Filipe L.A. Ribeiro, Universidade Nova de Lisboa

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=Bilin_Material&oldid=10636"